Question 203422: 1. The face of a $10 bill has an area that can be represented by the expression 10x² + 9x – 40.
(a) Factor the expression to find the dimensions of the bill.
(b) If x represents 32mm, what are the dimensions of the bill?
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! Since a $10 bill is a rectangle, its area would be found by multiplying the length and width. This is why you are asked to factor the expression for the area. By factoring the area expression, the factors then represent the length and width.
Factoring 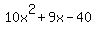 is not especially easy. What we want to end up with is something of the form: (ax + b)(cx + d) where- "a" and "c" are factors of 10 (the coefficient of x^2). So the possibilities are: 1 and 10, 2 and 5, -1 and -10, -2 and -5
- "b" and "d" are factors of -40 (the constant term). So the possibilities are: 1 and -40, -1 and 40, 2 and -20, -2 and 20, 4 and -10, -4 and 10, 5 and -8, -5 and 8
- (a*d) + (b*c) = 9 (the coefficient of the middle term).
Since there are so many combinations possible it can take a while to find the one that fits condition #3. The one that works is:
(2x + 5)(5x + (-8)) = (2x + 5)(5x - 8)
This works because
2 * 5 = 10
5 * -8 = -40
2 * -8 + 5 * 5 = -16 + 35 = 9
So  and length = 2x + 5 and width = 5x - 8 (or the other way around. It doesn't matter)
If x = 32 then
length = 2x + 5 = 2(32) + 5 = 64 + 5 = 69mm
width = 5x -8 = 5(32) - 8 = 160 - 8 = 152mm
|
|
|
