Question 1112891: A theater group made appearances in two cities. The hotel charge before tax in the second city was
$
1500
higher than in the first. The tax in the first city was
6.5
%
, and the tax in the second city was
3.5
%
. The total hotel tax paid for the two cities was
$
427.50
. How much was the hotel charge in each city before tax?
Answer by ikleyn(52803)   (Show Source):
You can put this solution on YOUR website! .
The system of 2 equations in 2 unknowns is THIS
-x + y = 1500, (1)
0.065x + 0.035y = 427.50. (2)
To solve it, I will apply the Elimination method. For it, I will multiply eq(1) by 0.065, keeping the eq(2) as is. You will get
-0.065x + 0.065y = 0.065*1500, (1')
0.065x + 0.035y = 427.50. (2')
Next step is to add equations (1') and (2'). In this way, the terms with "x" will cancel each other, and you will get a single equation
for the unknown "y" only
0.065y + 0.035y = 0.065*1500 + 427.50, or
0.1y = 525.
Hence, y= 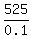 = 5250.
Answer. In the second city, the theater paid $5250 before tax.
In the first city, the theater paid 5250 - 1500 = 3750 dollars before tax.
Solved.
--------------
On the way, you learned on how the Elimination method works.
|
|
|
