Question 1073597: A turbo-prop plane flying with the wind flew 2100 mi in 5 h. Flying against the wind, the plane required 7 h to travel the same distance. Find the rate of the wind and the rate of the plane in calm air.
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let "u" be the speed of the plane at no wind (=same as in calm air), in mph.
Let "v" be the speed of wind.
Then the effective speed of the plane flying WITH the wind is (u+v) mph (relative to the ground).
the effective speed of the plane flying AGAINST the wind is (u-v) mph (relative to the ground).
According to the condition,
the plane effective speed is 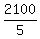 = 420 mph flying with the wind,
and effective speed is = 420 mph flying with the wind,
and effective speed is 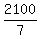 = 300 mph flying against the wind.
It gives you two equations
u + v = 420, (1)
u - v = 300. (2)
Add the two equations (both sides). You will get
2u = 420 + 300 = 720. Hence, u = = 300 mph flying against the wind.
It gives you two equations
u + v = 420, (1)
u - v = 300. (2)
Add the two equations (both sides). You will get
2u = 420 + 300 = 720. Hence, u = 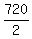 = 360.
Thus the speed of the plane at no wind is 360 mph.
Next, from the equation (1) v = 420 - u = 420 - 360 = 60 mph.
Thus the speed of the wind is 60 mph.
Answer. The speed of the plane at no wind is 360 mph.
The speed of the wind is 60 mph.
Check. The speed of the plane with the wind is 360 + 60 = 420 mph, and the flight time is = 360.
Thus the speed of the plane at no wind is 360 mph.
Next, from the equation (1) v = 420 - u = 420 - 360 = 60 mph.
Thus the speed of the wind is 60 mph.
Answer. The speed of the plane at no wind is 360 mph.
The speed of the wind is 60 mph.
Check. The speed of the plane with the wind is 360 + 60 = 420 mph, and the flight time is 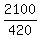 = 5 hours.
The speed of the plane against the wind is 360 - 60 = 300 mph, and the flight time is = 5 hours.
The speed of the plane against the wind is 360 - 60 = 300 mph, and the flight time is 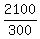 = 7 hours.
Checks ! = 7 hours.
Checks !
Solved.
It is a typical "tailwind and headwind" word problem.
See the lessons
- Wind and Current problems
- Wind and Current problems solvable by quadratic equations
- Selected problems from the archive on a plane flying with and against the wind
in this site.
In these lessons you will find the detailed solutions of many similar problems.
Learn how to solve similar problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".
|
|
|