Question 1062448: Please help me solve this problem.
Determine all the value of k such that the following system of linear equations has (i) Unique solution (ii) No solution and (iii) More than one solutions.
kx+y+z=1
x+ky+z=1
z+y+kz=1
I am stuck in reducing the augmented matrix into REF or RREF
Thank you in advance!
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Calculate the determinant of the matrix A =  .
If you are unfamiliar with it or want to refresh your knowledge, see the lesson
- Determinant of a 3x3 matrix
in this site.
The determinant is equal to .
If you are unfamiliar with it or want to refresh your knowledge, see the lesson
- Determinant of a 3x3 matrix
in this site.
The determinant is equal to 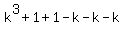 = = 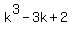 .
The general theory says:
If the determinant is not zero, then the system has a unique solution.
The degenerate cases are those when the determinant is zero:
d(k) = .
The general theory says:
If the determinant is not zero, then the system has a unique solution.
The degenerate cases are those when the determinant is zero:
d(k) = 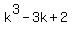 = 0.
One root of this equation is k = 1.
Hence, the polynomial is multiple of (k-1), and the ratio = 0.
One root of this equation is k = 1.
Hence, the polynomial is multiple of (k-1), and the ratio 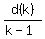 is is 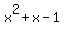 .
Then the two other roots of the determinant are the zeroes of this quadratic polynomial .
Then the two other roots of the determinant are the zeroes of this quadratic polynomial 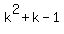 .
You can easily find these zeroes using the quadratic formula: .
You can easily find these zeroes using the quadratic formula:
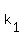 = = 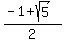 and and 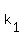 = = 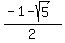 .
Next, if k = 1, your original system consists of three identical equations.
Hence, the system has infinitely many solutions at k = 1.
If k = .
Next, if k = 1, your original system consists of three identical equations.
Hence, the system has infinitely many solutions at k = 1.
If k = 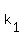 or k = or k = 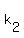 , then the system has infinitely many solutions, too.
Indeed, if you add all three equations at these values of k, you will get the equation
(k+2)x + (k+2)y + (k+2)z = 3, or
x + y + z = , then the system has infinitely many solutions, too.
Indeed, if you add all three equations at these values of k, you will get the equation
(k+2)x + (k+2)y + (k+2)z = 3, or
x + y + z = 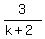 . (*)
Now distract the equation (1) from (*), and you will find the solution for x.
Distract then the equation (2) from (*), and you will find the solution for y.
Finally, distract the equation (3) from (*), and you will find the solution for z.
Thus the system has at least one solution for k = . (*)
Now distract the equation (1) from (*), and you will find the solution for x.
Distract then the equation (2) from (*), and you will find the solution for y.
Finally, distract the equation (3) from (*), and you will find the solution for z.
Thus the system has at least one solution for k = 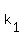 and/or k = and/or k = 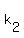 , having the determinant equal to zero at these values of k.
It is enough for the system to have infinitely many solutions then. , having the determinant equal to zero at these values of k.
It is enough for the system to have infinitely many solutions then.
Answer. The system has infinitely many solutions at k = 1, k = 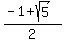 and k = and k = 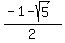 . .
The system has a unique solution for all other values of k.
------------------------------
The useful references on this theme are these lessons
- Determinant of a 3x3 matrix
- HOW TO solve system of linear equations in three unknowns using determinant (Cramer's rule)
- Solving systems of linear equations in three unknowns using determinant (Cramer's rule)
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic
"3x3-Matrices, determinants, Cramer's rule for systems in three unknowns"
|
|
|