SOLUTION: Find all zeros of f(x)=x^3-x^2+x-21 and write a complete linear factorization of f (x)

One root is x= 3. You can check it directly.

It means that (x-3) is the factor of the polynomial which divides the polynomial without a remainder ("The Remainder Theorem").


So, make a long division and find the quotient .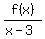


It is a quadratic polynomial.


Check it discriminant to determine if this quadratic has real roots.

     The polynomial remainder theorem states that the remainder of the division of a polynomial f(x) by a linear polynomial  x-a is equal to  f(a).      

     In particular,  x-a is a divisor of  f(x) if and only if f(a)=0.