Lesson Counting calories and grams of fat in combined food

This Lesson (Counting calories and grams of fat in combined food) was created by by ikleyn(52781)

: View Source, Show
About ikleyn:

Counting calories and grams of fat in combined food

Problem 1

Two foods are combined to give a total of 1600 calories and 17 g of fat. The first food has 200 calories per ounce and 3 g of fat per ounce,
the second food has 250 calories per ounce and 2 g of fat per ounce. How many ounces of each food is used?

Let x be the amount of the first food (in ounces) and y be the amount of the second food.


From the condition, you have these two equation

200*x + 250*y = 1600,     (1)    (counting calories)
  3*x +   2*y =   17.     (2)    (counting grams of fat)


To solve the system, multiply eq(1) by 3 (both sides). Multiply eq(2) by 200 (both sides). The modified system is

600x + 750y = 4800,       (3)
600x + 400y = 3400.       (4)


Now subtract eq(4) from eq(3)  (both sides).  The terms with "x" will cancel each other, 
and you will get a single equation for the unknown "y" only:


350y = 4800 - 3400,   or

350y = 1400  ====>  y = 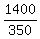 = 4.


Thus you just found that 4 ounces of the second food must be used.


To find "x", substitute the found value y= 4 into eq(2). You will get

3x + 2*4 = 17  ====>  3x = 17 - 2*4 = 9  ====>  x =  = 3.


Answer.  3 ounces of the first food and 4 ounces of the second food.

In the solution I used the Elimination method, so you could see how it worked.

My other lessons in this site on solving systems of two linear equations in two unknowns (Algebra-I curriculum) are
    - Solution of the linear system of two equations in two unknowns by the Substitution method
    - Solution of the linear system of two equations in two unknowns by the Elimination method
    - Solution of the linear system of two equations in two unknowns using determinant
    - Geometric interpretation of the linear system of two equations in two unknowns
    - Useful tricks when solving systems of 2 equations in 2 unknowns by the Substitution method
    - Solving word problems using linear systems of two equations in two unknowns

    - Word problems that lead to a simple system of two equations in two unknowns
    - Oranges and grapefruits
    - Using systems of equations to solve problems on tickets
    - Three methods for solving standard (typical) problems on tickets
    - Using systems of equations to solve problems on shares
    - Using systems of equations to solve problems on investment
    - Two mechanics work on a car
    - The Robinson family and the Sanders family each used their sprinklers last summer
    - Roses and vilolets
    - A theater group made appearances in two cities
    - Exchange problems solved using systems of linear equations
    - Typical word problems on systems of 2 equations in 2 unknowns
    - HOW TO algebraize and solve these problems on 2 equations in 2 unknowns
    - One unusual problem to solve using system of two equations
    - Non-standard problem with a tricky setup
    - Sometimes one equation is enough to find two unknowns in a unique way
    - Solving mentally word problems on two equations in two unknowns
    - Solving systems of non-linear equations by reducing to linear ones
    - Solving word problems for 3 unknowns by reducing to equations in 2 unknowns
    - System of equations helps to solve a problem for the Thanksgiving day
    - Using system of two equations to solve the problem for the day of April, 1

    - OVERVIEW of lessons on solving systems of two linear equations in two unknowns

Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.

This lesson has been accessed 2997 times.