SOLUTION: Find the inverse matrix: -9 5 6 3

Algebra ->  Conversion and Units of Measurement -> SOLUTION: Find the inverse matrix: -9 5 6 3      Log On


   

Question 551232: Find the inverse matrix: -9 5
6 3
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Solved by pluggable solver: Finding the Inverse of a 2x2 Matrix

To find the inverse of the matrix A=%28matrix%282%2C2%2C-9%2C5%2C6%2C3%29%29, we can follow these steps:

Step 1) Find the determinant



The determinant of 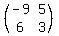%28matrix%282%2C2%2C-9%2C5%2C6%2C3%29%29 is abs%28matrix%282%2C2%2C-9%2C5%2C6%2C3%29%29=-57. So this means that d=-57

Step 2) Swap the values



Now switch the highlighted values %28matrix%282%2C2%2Chighlight%28-9%29%2C5%2C6%2Chighlight%283%29%29%29 to get %28matrix%282%2C2%2Chighlight%283%29%2C5%2C6%2Chighlight%28-9%29%29%29

Step 3) Change the sign



Now change the sign of the highlighted values %28matrix%282%2C2%2C3%2Chighlight%285%29%2Chighlight%286%29%2C-9%29%29 to get %28matrix%282%2C2%2C3%2Chighlight%28-5%29%2Chighlight%28-6%29%2C-9%29%29

Step 4) Multiply by the inverse of the determinant



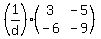
Multiply by 1%2Fd to get %281%2Fd%29%28matrix%282%2C2%2C3%2C-5%2C-6%2C-9%29%29

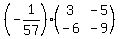
Plug in d=-57 to get %28-1%2F57%29%28matrix%282%2C2%2C3%2C-5%2C-6%2C-9%29%29

Step 5) Multiply -1%2F57 by every element in the matrix (simplify and reduce if possible)



Multiply -1%2F57 by EVERY element to get

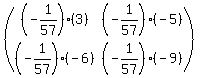
Multiply to get %28matrix%282%2C2%2C3%2F-57%2C-5%2F-57%2C-6%2F-57%2C-9%2F-57%29%29

Reduce each element: 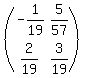%28matrix%282%2C2%2C-1%2F19%2C5%2F57%2C2%2F19%2C3%2F19%29%29


=================================================================


Answer:

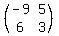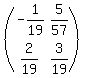
So the inverse of %28matrix%282%2C2%2C-9%2C5%2C6%2C3%29%29 is %28matrix%282%2C2%2C-1%2F19%2C5%2F57%2C2%2F19%2C3%2F19%29%29

This means that if A=%28matrix%282%2C2%2C-9%2C5%2C6%2C3%29%29 then A%5E%28-1%29=%28matrix%282%2C2%2C-1%2F19%2C5%2F57%2C2%2F19%2C3%2F19%29%29