Question 468953: carrie can inpsect a case of watches in 5 hours, james can inspect the same case in 3 hours. after working alone for 1 hour, carrie takes a break. after taking a 40 minute break, carrie and james work together to inspect the remaining watches. how long do carrie and james work together to complete the job?
Found 2 solutions by Edwin McCravy, robertb:
Answer by Edwin McCravy(20077)   (Show Source): (Show Source):
You can put this solution on YOUR website! carrie can inpsect a case of watches in 5 hours, james can inspect the same case in 3 hours. after working alone for 1 hour, carrie takes a break. after taking a 40 minute break, carrie and james work together to inspect the remaining watches. how long do carrie and james work together to complete the job?
Make this chart
No. of cases
inspected or Time
fraction of a in Rate in
case inspected hours Cases/hour
Carrie working alone | | |
James working alone | | |
Both before Carrie's break | | |
James alone during Carrie's break | | |
Both after Carries break | | |
1. Let x be the answer, so put x for the time for both after Carrie's break.
2. On the top line, since Carrie can inspect 1 case of watches in 5 hours,
put 1 for the no. of cases inspected, and 5 for the number of hours
3. On the next to the top line, since James can inspect 1 case of watches
in 3 hours, put 1 for the no. of cases inspected, and 5 for the number of hours.
4. Since both worked alone for 1 hour before Carrie took a break, put 1 for
the no. of hours before Carrie's break.
5. For the 40 minutes Carrie was on break, we would put that 40 minutes, but
to avoid mixing minutes and hours we change 40 minutes to 40/60 of an hour,
or 2/3 of an hour, so we put 2/3 for the time James worked alone during
Carrie's break.
No. of cases
inspected or Time
fraction of a in Rate in
case inspected hours Cases/hour
Carrie working alone | 1 | 5 |
James working alone | 1 | 3 |
Both before Carrie's break | | 1 |
James alone during Carrie's break | | 2/3 |
Both after Carries break | | x |
Now we fill in the first two rates by dividing no. of cases by time. So
we fill them is as 1/5 and 1/3:
No. of cases
inspected or Time
fraction of a in Rate in
case inspected hours Cases/hour
Carrie working alone | 1 | 5 | 1/5
James working alone | 1 | 3 | 1/3
Both before Carrie's break | | 1 |
James alone during Carrie's break | | 2/3 |
Both after Carries break | | x |
1. We now fill in the rate for James alone during Carrie's break also
as 1/3 cases/hr.
2. We also fill in the rate when both work together by adding their
rates. 1/5 + 1/3 = 3/15 + 5/15 = 8/15 so put 8/15 for both rates
for both working together both before and after the break:
No. of cases
inspected or Time
fraction of a in Rate in
case inspected hours Cases/hour
Carrie working alone | 1 | 5 | 1/5
James working alone | 1 | 3 | 1/3
Both before Carrie's break | | 1 | 8/15
James alone during Carrie's break | | 2/3 | 1/3
Both after Carries break | | x | 8/15
Now we fill in the remaining no. of cases inspected (actually fraction
of a case inspected) by multiplying the hours by the rate in cases/hour.
1. The fraction of a case when both works before Carrie's break is
(1)(8/15) = 8/15 for the fraction of a case inspected before Carrie's
break.
2. The fraction of a case when both works before Carrie's break is
(2/3)(1/3) = 2/9 for the fraction of a case inspected by James alone
during Carrie's break.
3. The fraction of a case inspected by both after Carrie's break is
indicated by multiplying 8 by x/15 giving (8/15)x.
Fill these in:
No. of cases
inspected or Time
fraction of a in Rate in
case inspected hours Cases/hour
Carrie working alone | 1 | 5 | 1/5
James working alone | 1 | 3 | 1/3
Both before Carrie's break | 8/15 | 1 | 8/15
James alone during Carrie's break | 2/9 | 2/3 | 1/3
Both after Carries break | (8/15)x | x | 8/15
Now we make the equation by adding the three fractions of a case,
before, during, and after Carrie's break, and equate that to 1
whole case:
 + + + + x = 1
Multiply through by LCD of 45
24 + 10 + 24x = 45
34 + 24x = 45
24x = 11
x = x = 1
Multiply through by LCD of 45
24 + 10 + 24x = 45
34 + 24x = 45
24x = 11
x = 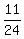 So the answer is
So the answer is 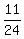 ths of an hour or or ths of an hour or or  minutes.
Edwin minutes.
Edwin
Answer by robertb(5830)   (Show Source): (Show Source):
|
|
|