Question 857211: Please help me solve this problem:
Find all complex square roots of i. in other words find all complex solutions of x^2 = i
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! This may be only part of the answer, but  if if  . .
How?
Draw a unit circle. The horizontal axis is Real and the vertical axis is Imaginary. Horizontal intercepts are 1 and -1. Vertical intercepts are i and -i. Think of multiplications by whole number powers of i to be rotations starting at (1,0). If 1*1, get 1. If 1*-1, get -1. If 1*i, get i. If 1*(i)(i), get same as 1*(-1) which is -1. Thinking this way, the way to go from negative 1 to HALF WAY from negative 1 to positive 1 is the take square root of -1.
In that same way, if you start with  , and you want what is x, this is like starting at (0,i) on this complex unit circle, and rotating half-way from (0,i) to (1,0). This puts your point on an angle of positive , and you want what is x, this is like starting at (0,i) on this complex unit circle, and rotating half-way from (0,i) to (1,0). This puts your point on an angle of positive  . The coordinates on this point are as (cos(pi/4),i*sin(pi/4)), which you can represent as . The coordinates on this point are as (cos(pi/4),i*sin(pi/4)), which you can represent as 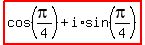 . .
|
|
|