what is the limit of [-4(x-5)(x+2)]/[-x(x+2)] that x approaches to infinity.
 Cancel the negative signs. That makes me wonder
if you copied it right. Since you're taking
calculus, it seems odd that your teacher would be
testing you on something so elementary as to whether
you know that a negative divided by a negative is a
positive. But let's cancel them to get rid of them:
Cancel the negative signs. That makes me wonder
if you copied it right. Since you're taking
calculus, it seems odd that your teacher would be
testing you on something so elementary as to whether
you know that a negative divided by a negative is a
positive. But let's cancel them to get rid of them:
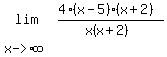 Now we need to multiply all that out to remove the
parentheses:
Now we need to multiply all that out to remove the
parentheses:
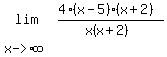

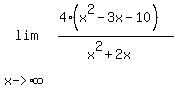
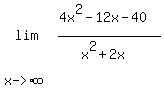 Now the highest power of x that appears in numerator
or denominator is is x², so we divide every term in
the numerator and denominator by x²:
Now the highest power of x that appears in numerator
or denominator is is x², so we divide every term in
the numerator and denominator by x²:
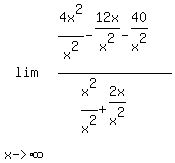 and simplify
and simplify
 Now we know that
Now we know that 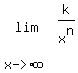

 fo any constant k,
and any positive integer n, so each of the fraction terms,
fo any constant k,
and any positive integer n, so each of the fraction terms,
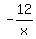 ,
, , in the numerator and
, in the numerator and 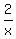 in
the denominator all approach 0 as x approaches infinity, so
we have:
(4-0-0)/(1) = 4
Answer: 4
Edwin
in
the denominator all approach 0 as x approaches infinity, so
we have:
(4-0-0)/(1) = 4
Answer: 4
Edwin