To find the argument  ,
,
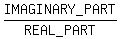



 Write
Write  as
as 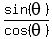
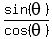

 Cross-multiply
Cross-multiply
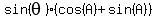

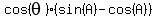
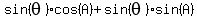

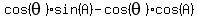 Rearrange the equation:
Rearrange the equation:
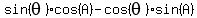

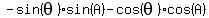
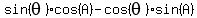

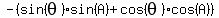
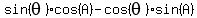

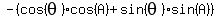
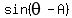

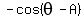 Divide both sides by
Divide both sides by 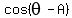
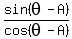


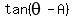


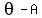

 ,
, 


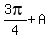 ,
, 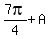 To find the modulus or absolute value r:
To find the modulus or absolute value r:


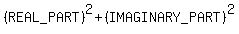


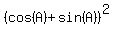

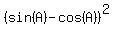


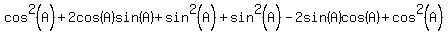 Using the identity cosineČ + sineČ = 1, the right side is just 2
rČ = 2
r = √2
Polar forms:
√2[cos(
Using the identity cosineČ + sineČ = 1, the right side is just 2
rČ = 2
r = √2
Polar forms:
√2[cos(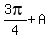 ) + i·sin(
) + i·sin(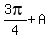 )]
√2[cos(
)]
√2[cos(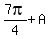 ) + i·sin(
) + i·sin(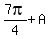 )]
Edwin
)]
Edwin