Find all zeros of h(x)= x³ - 9x² + 19x - 35
If there are any rational zeros they have to be ± a divisors of 35.
So we try 5
5|1 -9 19 -35
| 5 -20 -5
1 -4 -1 -40
Nope, 5 is not a zero.
So try 7
7|1 -9 19 -35
| 7 -14 35
1 -2 5 0
Yep that's a zero, so we have now factored h(x) as
h(x)= x³ - 9x² + 19x - 35
h(x)= (x - 7)(x² - 2x + 5)
Set each factor = 0
x - 7 = 0 x² - 2x + 5 = 0
x = 7
The first gives back the factor we just found.
The second must be solved with the quadratic formula:
x =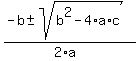 
x = 
x =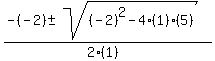 
x = 
x =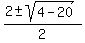 
x = 
x =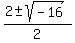 
x = 
x = 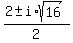1 ± 2i
The 3 zeros are 7, 1 + 2i, and 1 - 2i
--------------------------------------------
Find all zeros of
f(x)= x³ - 2x² + 25x - 50
That one can be factored by grouping:
Factor x² out of the first two terms and 25 out of the last two:
f(x) = x²(x - 2) + 25(x - 2)
Factor (x - 2) out of both terms:
f(x) = (x - 2)(x² + 25)
Set each = 0:
x - 2 = 0
x = 2
x² + 25 = 0
x² = -25
x = 
x = 
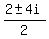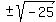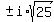x = ±5i
The three zeros are 2, 6i, and -5i
Edwin
