I'll just do (2) and you can use it as a model to
do (1).
Let's draw the picture of that complex number as a
right triangle on a graph. 
where 
, 
(a) 
.
Sometimes this is called the "modulus". This is the length of
the hypotenuse of that right triangle. We find it the same way
we always find the hypotenuse, the Pythagorean theorem:
We label the hypotenuse 
and this is the same as
(b) find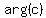 
when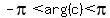 
"Argument" means "angle" (you can remember it because "argument"
and "angle" both start with "a" and their third letters are "g")
Now since we are told that the argument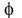 
is between 
and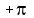 
, we must take the argument as a negative angle
measured by rotating clockwise from the right side of the x-axis,
indicated by the blue arc below labeled 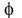, "phi".
It should be q, "theta", but I can't
get that Greek letter on the notation program for this site, so
I'll use 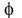instead.
Since the triangle is an isosceles right triangle, its interior
angles are 
or 
in radians. However since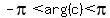
tells us that the rotation is clockwise from the right
side of the x-axis, the angle is taken as negative. Thus we
take it as 
and we label it:
(c) write in polar form:
Since 
, therefore 
and since 
, therefore 
So 
and we can factor out 
and get:
This is the polar form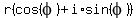 
of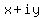 
Therefore since and
(d) 
or (sqrt(2)-i*sqrt(2))^6}}}
DeMoivre's theorem says:
Therefore:
Since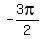 
is coterminal with 
, we have
Edwin
