Question 1207322: f (x) is polynomial function, f '(x) + int f (x) dx = x ^4 + 13 x ^2 + 2. Find f (x)
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
f (x) is  polynomial function, f '(x) + int f (x) dx = x ^4 + 13 x ^2 + 2, polynomial function, f '(x) + int f (x) dx = x ^4 + 13 x ^2 + 2,
Find f(x)
~~~~~~~~~~~~~~~~~~~~~~
We want to find f(x) as a polynomial f(x) =  + + 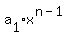 + . . . + + . . . +  .
Taking derivative decreases the degree of a polynomial by one unit.
Taking antiderivative increases the degree of a polynomial by one unit.
Since the sum f ' (x) + int f (x) dx is a polynomial of degree 4,
----------------------
it means that the sough polynomial f(x) is of degree 3:
f(x) = ax^3 + bx^2 + cx + d.
Then
f ' (x) = .
Taking derivative decreases the degree of a polynomial by one unit.
Taking antiderivative increases the degree of a polynomial by one unit.
Since the sum f ' (x) + int f (x) dx is a polynomial of degree 4,
----------------------
it means that the sough polynomial f(x) is of degree 3:
f(x) = ax^3 + bx^2 + cx + d.
Then
f ' (x) = 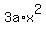 + 2bx + c,
int f(x) dx = + 2bx + c,
int f(x) dx = 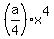 + + 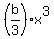 + + 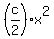 + dx + E.
So, in the sum f ' (x) + int f(x) dx
----------------------
(a) coefficient at + dx + E.
So, in the sum f ' (x) + int f(x) dx
----------------------
(a) coefficient at  is is 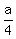 It gives an equation It gives an equation
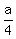 = 1; hence a = 4.
(b) coefficient at = 1; hence a = 4.
(b) coefficient at  is 0. It gives an equation is 0. It gives an equation
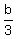 = 0; hence b = 0.
(c) coefficient at = 0; hence b = 0.
(c) coefficient at  is 13. It gives an equation is 13. It gives an equation
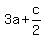 = 13, or = 13, or  = 13 ---> = 13 --->  = 13 - 12 = 1 ---> c = 2.
(d) coefficient at = 13 - 12 = 1 ---> c = 2.
(d) coefficient at  is 0. It gives an equation
2b + d = 0, which implies 2*0 + d = 0; hence, d = 0.
+------------------------------------------------------------+
| At this point, the problem is just solved to the end. |
| a = 4; b = 0; c = 2; d = 0. |
+------------------------------------------------------------+
The sough polynomial is f(x) = 4x^3 + 2x. ANSWER
CHECK. The derivative is f ' (x) = is 0. It gives an equation
2b + d = 0, which implies 2*0 + d = 0; hence, d = 0.
+------------------------------------------------------------+
| At this point, the problem is just solved to the end. |
| a = 4; b = 0; c = 2; d = 0. |
+------------------------------------------------------------+
The sough polynomial is f(x) = 4x^3 + 2x. ANSWER
CHECK. The derivative is f ' (x) = 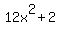 .
The anti-derivative is F(x) = .
The anti-derivative is F(x) = 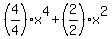 = = 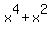 .
The sum f ' (x) + F(x) = .
The sum f ' (x) + F(x) = 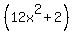 + + 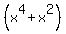 = = 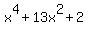 . ! correct ! . ! correct !
Solved.
Do not accept any other  answer. answer.
--------------
The solution by Edwin is INCORRECT.
To make sure that it is incorrect, simply take the antiderivative of his leading term 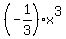 . .
This antiderivative is 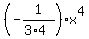 = = 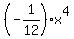 , and no other arguments are needed anymore. , and no other arguments are needed anymore.
|
|
|