SOLUTION: Graph the given arc. Let 𝐶: 𝑧 = 𝑧(𝑡), 0 ≤ 𝑡 ≤ 4, defined by 𝑧 = {𝑡 − 𝑖𝑡 , 0 ≤ 𝑡 ≤ 2 𝑡 − 𝑖 , 2 < 𝑡 ≤ 4

This is a piecewise graph with parameter t.



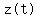We will use a two-dimensional Cartesian plane, and identify the 
point with coordinates (x,y) with the complex number z = x+iy. 
Here, 'i' is the imaginary unit and is identified with the point 
with coordinates (0,1).

We normally think of an "arc" as a curved line.  However in complex
analysis we use a more general definition. A set of points in the 
complex plane is called "an arc" if x = x(t) and y = y(t) for a<t<b 
where x(t) and y(t) are continuous functions of real parameter t. 
We denote an arc C as z(t)=x(t)+iy(t) for a<t<b.

The left part of the graph where t goes from t=0 to t=2,
is a line segment from 0-i*0, or the point (0,0) to 2-i*2, or the 
point (2,-2), where the segment includes both its endpoints.

 

The right part of the graph where t goes from t=2 to t=4,
is a line segment from 2-i, or the point (2,-1) to 4-i, or 
the point (4,-1), where the segment does not include its 
left endpoint, but does include its right endpoint.

 

Edwin