Question 1205493: Solve : x! × y! = 120 × (xy)!
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve : x! × y! = 120 × (xy)!
~~~~~~~~~~~~~~~~~~~~~~
There are two solutions.
One solution is x= 5, y= 0.
Other solution is x= 0, y= 5.
Let's prove first that x= 5, y= 0 is the solution.
Indeed, then x! = 5! = 120;
y! = 0! = 1 ( by the definition of 0! )
thus left side is x! * y! = 120 * 1 = 120.
Next, for the right side (xy)! = (5*0)! = 0! = 1 ( again, by the definition of 0! ),
and thus left side, 120, is equal to the right side, which is 120, too.
For other solution, x= 0, y= 5, the proof is symmetric.
Solved.
--------------------
Edwin,
thanks for this valuable addition.
Happy new year!
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn has found two solutions, (x,y) = (5,0) and (x,y) = (0,5)
but has failed to show that there are no other solutions. But it is
necessary to show that there are no other solutions, not just to
find two solutions and verify that they are both solutions.
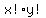  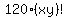 Those will be the only solutions if and only if
Those will be the only solutions if and only if
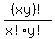 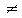  , for , for 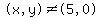 and and 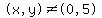 Assume
Assume  If x = 0, then
If x = 0, then 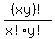  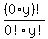  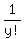 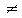  , except for the solution (x,y) = (0,5)
If x = 1, then , except for the solution (x,y) = (0,5)
If x = 1, then 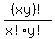  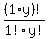  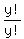   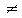  If
If  then then 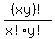  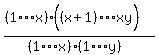  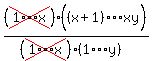  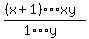 The numerator of that last fraction has xy-x indicated factors and the
denominator has y factors.
Since
The numerator of that last fraction has xy-x indicated factors and the
denominator has y factors.
Since  and and  , ,
 Subtract 1 from both sides
Subtract 1 from both sides
 Divide both sides by x-1
Divide both sides by x-1







 This proves the numerator has at least as many indicated factors as the
denominator. The first x factors of the denominator are, respectively, less
than or equal to the first x factors of the numerator. The remaining indicated
factors of the numerator, if any, are even greater. Therefore, the numerator of
the fraction
This proves the numerator has at least as many indicated factors as the
denominator. The first x factors of the denominator are, respectively, less
than or equal to the first x factors of the numerator. The remaining indicated
factors of the numerator, if any, are even greater. Therefore, the numerator of
the fraction 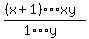 is greater than the denominator, and the fraction
is greater than or equal to 1, and therefore not equal to is greater than the denominator, and the fraction
is greater than or equal to 1, and therefore not equal to  .
The case .
The case  is proved by symmetry.
Therefore the 2 solutions Ikleyn found above are the ONLY solutions.
Edwin is proved by symmetry.
Therefore the 2 solutions Ikleyn found above are the ONLY solutions.
Edwin
|
|
|