Question 1204850: Find :
1) (- 4)^(6/4)
2) (root[6]((-8))^2
Found 4 solutions by MathLover1, MathTherapy, greenestamps, ikleyn:
Answer by MathLover1(20850)   (Show Source):
Answer by MathTherapy(10552)  (Show Source):
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
For this post, tutor @MathTherapy has provided another of his responses claiming the answer from another tutor is wrong, without providing his answer. That kind of response is of no help to the student; it only serves to demonstrate his perceived superiority.
In fact the answer from the other tutor is right.
To get a real answer, the expression would have to be written differently.
But to get that answer from the given expression, you would have to perform the exponentiation "(-4)^6" before simplifying inside the parentheses to change the fraction 6/4 to 3/2. Standard order of operations says we simplify inside parentheses before doing the exponentiation.
So the real answer "8" is not right; the correct answer is the imaginary "-8i".
Answer by ikleyn(52788)  (Show Source):
You can put this solution on YOUR website! .
Find :
1) (- 4)^(6/4)
2) (root[6]((-8))^2
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Although the problem is silent about it, it is clear that in both cases the question is
Find all values of these expressions in complex domain.
So, I will solve the problem (part 1) in this formulation.
Also, it is clear that the problem is not for a school student, because a normal school student does not understand
its meaning (together with his/her teacher) - it is for, let say, a University level students majoring in Math,
who study (or just studied) complex numbers analysis at the proper level.
Question 1
(-4)^(6/4) = (-4)^(3/2) = ((-4)^3)^(1/2) =  =  .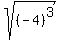
This square root of the negative number -64 has 2 (TWO) values in complex numbers.
One value is 8i. Another value -8i.
ANSWER. (- 4)^(6/4) has two values in complex domain.
One value is 8i. Another value is -8i.
So, when other tutors says that 8i is the solution, it is correct, but only partly correct.
Full complete correct answer is that there are TWO values, 8i and -8i.
. . . . . . . . . . . . . . . . . . . .
Regarding second question, there is a FATAL ERROR in its formulation: the parentheses are UNBALANCED,
so the meaning of the formula is not determined and CAN NOT be determined without a fundamental repair.
=======================
The lesson to learn from my post to question 1 is that in complex domain taking square root
is not an operation "one value to one value". It is an operation "one value to TWO values".
Similar as to cubic root in complex domain is not an operation "one value to one value".
It is an operation "one value to three values".
This understanding is one of basic conceptions, that a University student should
get from the University class on complex analysis ("on complex numbers").
In reality, only small part of University students really gets this understanding.
Those who really get such understanding, are either those who become professional mathematicians
of the "professorship level" with peer-reviewed articles/textbooks/monographs in the area,
or theoretical physicists, who use "phases" in their work.
Of the school teachers, 99.9% of them do not understand it even at conceptual level -
- therefore, it is useless even to discuss this matter with them.
|
|
|
