Question 1181501: Check that (2 + i) is a root of (z^4) + (2(z^3)) - (9(z^2)) - 10z + 50 = 0. What are the remaining 3 roots?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Check that (2 + i) is a root of (z^4) + (2(z^3)) - (9(z^2)) - 10z + 50 = 0. What are the remaining 3 roots?
~~~~~~~~~~~~~~~~~
Yes, from the first glance, it is almost impregnable fortress.
Let apply a military ruse.
Our polynomial is with real ( even with integer (!) ) coefficients.
Hence, if (2+i) is a root, then (2-i) is a root, too (!)
If so, then our polynomial must be divisible by (z-(2+i))*(z-(2-i)) = ((z-2)-i)*((z-2)-i) = (z-2)^2 + 1 = z^2 - 2z +5.
Lets make long division to check if it is TRUE:
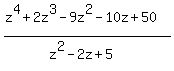 = = 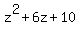 with NO REMAINDER (!)
Thus we checked that the given polynomial is a multiple of the polynomial z^2 - 2z + 5.
It means that (2+i) REALLY is a root of the given polynomial (without direct calculations (!))
+------------------------------------------------------------------------------------------------+
| So, we know now that |
| |
| (2+i) really is the root of the given polynomial; |
| (2-i) is the other root; |
| one factor to the given polynomial is z^2 - 2z + 5 with the roots (2+i) and (2-i); |
| the other factor is the polynomial z^2 +6z + 10. |
+------------------------------------------------------------------------------------------------+
At this point, the last step to do is to find the roots of the quadratic polynomial z^2 + 6z + 10.
Apply the quadratic formula to get with NO REMAINDER (!)
Thus we checked that the given polynomial is a multiple of the polynomial z^2 - 2z + 5.
It means that (2+i) REALLY is a root of the given polynomial (without direct calculations (!))
+------------------------------------------------------------------------------------------------+
| So, we know now that |
| |
| (2+i) really is the root of the given polynomial; |
| (2-i) is the other root; |
| one factor to the given polynomial is z^2 - 2z + 5 with the roots (2+i) and (2-i); |
| the other factor is the polynomial z^2 +6z + 10. |
+------------------------------------------------------------------------------------------------+
At this point, the last step to do is to find the roots of the quadratic polynomial z^2 + 6z + 10.
Apply the quadratic formula to get
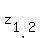 = = 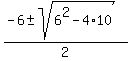 = = 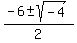 = = 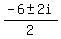 = -3 +- i.
The problem is just solved in full.
We checked and proved that 2+i is the root.
From it, we concluded that 2-i is the root, too.
And finally, we found two remaining roots -3+i and -3-i. = -3 +- i.
The problem is just solved in full.
We checked and proved that 2+i is the root.
From it, we concluded that 2-i is the root, too.
And finally, we found two remaining roots -3+i and -3-i.
Solved, answered, carefully explained and totally completed.
T R I U M P H (!)
//////////////
In his post, tutor @greenestamps writes (cited)
In the hopes of making the problem easier, we can, as the other tutor did, assume ("hope") that the polynomial has real coefficients.
I want to HIGHLIGHT that it is not an assumption: the given polynomial REALLY has integer (hence, real) coefficients.
It is not an assumption: it is a FACT.
Answer by greenestamps(13200)   (Show Source): (Show Source):
|
|
|