Question 1102473: For each statement,state whether it is always,sometimes,or never true, and briefly justify each answer:
N) If 𝑞 ∈ N, then there exists a number 𝑝 ∈ N such that 𝑝2 = 𝑞.
Z) If 𝑞 ∈ Z, then there exists a number 𝑝 ∈ Z such that 𝑝2 = 𝑞.
Q) If 𝑞 ∈ Q, then there exists a number 𝑝 ∈ Q such that 𝑝2 = 𝑞.
R) If 𝑞 ∈ R, then there exists a number 𝑝 ∈ R such that 𝑝2 = 𝑞.
C) If 𝑞 ∈ C, then there exists a number 𝑝 ∈ C such that 𝑝2 = 𝑞.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! N) 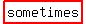 true. true.
 = the set of natural numbers, or counting numbers, {1, 2, 2, ...} = the set of natural numbers, or counting numbers, {1, 2, 2, ...}
For  , there is , there is  such that such that  , ,
but for  , if , if  , then , then  does not belong to set N. does not belong to set N.
Z)  true. true.
 = the set of integers = the set of integers
For  , there is , there is  such that such that  , ,
but for  , if , if  , then , then  does not belong to set Z, does not belong to set Z,
and for integer  there is neither integer, nor rational, nor real number there is neither integer, nor rational, nor real number  such that such that  . .
Q)  true. true.
 = the set of rational numbers. = the set of rational numbers.
All the examples above still work the same way,
so it is still sometimes true, and sometimes not true.
No need to look for more examples.
R)  true. true.
 = the set of real numbers. = the set of real numbers.
For any non-negative real number  , ,
there are always two real numbers  , such that , such that  . .
However, for negative numbers, that is not true.
For  , there is no real number , there is no real number  such that such that  . .
C)  true. true.
 = the set of complex numbers. = the set of complex numbers.
For every complex number  there are always two complex numbers there are always two complex numbers  and and 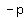 , such that , such that  . .
Any complex number can be written as  , ,
with  being a non-negative real number, being a non-negative real number,  , ,
and  being an angle with being an angle with  , ,
For complex number  , ,  . .
For  , ,  too. too.
and  p= p=
|
|
|