Question 1086726: (3x/2x-1)-(4x/3x+1)=(18/6x^2-x-1)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I believe that you mean
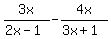  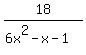 , ,
and that is the problem I am going to try rto solve.
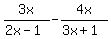  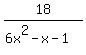
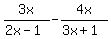  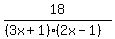
Multiplying both sides of the equation times  , we get , we get






So, either  <--> <-->  , ,
or  <--> <-->  . .
NOTE:
A group of conventions often called "order of operations"
is taught (but not always clearly explained) in beginning algebra.
We use a lot of conventions in math (as in any language).
The symbols for numbers and operations are the first you were taught.
After that, in elementary school,
you could show solutions to simple problems one step at a time
(one mathematical operation at a time).
That is like being able to talk a single word at a time,
before we speak in whole sentences.
It is a good first step, but hopefully we grow to be able to do more.
After learning the basics, you want to be able to talk/write a whole sentence,
and to be able to communicate efficiently,
we had to agree on some conventions.
We agreed on what "man bites dog" and what "dog bites man" mean.
We also agreed that the expression for the total cost in dollars at the pharmacy of
5 cans of tuna, 2 bags of potato chips, 3 pack of batteries and 1 tube of toothpaste
would be written as
5 X 1 + 2 X 2 + 3 X 7 + 4
rather than
(5 X 1) + (2 X 2) + (3 X 7) + 4 .
That agreement saves brackets, ink, and handwriting work.
By convention,
whatever is between plus and minus signs is calculated first,
unless parentheses are involved.
Parentheses are useful when we need them.
Often undeclared (or not emphasized enough) conventions
give other symbols similar effort-saving usefulness.
Those horizontal lines we use to separate expressions used as numerator and denominator
are agreed to includes invisible parentheses around numerator and denominator,
so we can save ink and effort when we write rational expressions on two lines.
That agreement was a great invention.
However, sometimes we cannot write double-decker expressions,
and then we need to wrap those numerators and denominators in brackets.
The expressions 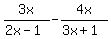 and and 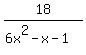 , written in one line , written in one line
(as you would enter numbers in a calculator when evaluating those expressions),
should be written with strategically placed parentheses indicating what parts to calculate first,
as in 3x/(2x-1)-4x/(3x+1) and 18/(6x^2-x-1) .
|
|
|