Question 1078164: Do the sum of the n nth roots of a complex number z always equals zero? Show this using the examples below.
1. Find the cube roots of -i
2. Find the fourth roots of 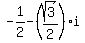
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52787)   (Show Source): (Show Source):
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
She used trigonometry, but I think you can use just algebra,
and no trig. Think I'll try to do it that way, just for fun,,
since she's already done it the trig way.
Let
(a + bi)³ = -i, where a, b are real.
a³ + 3a²bi + 3ab²i² + b³i³ = -i
a³ + 3a²bi - 3ab² - b³i = -i
Equating real parts: | Equating imaginary parts:
|
a³ - 3ab² = 0 | 3a²b - b³ = -1
a(a²-3b²) = 0 |
a = 0; a²-3b² = 0 |
a² = 3b² -> 3(3b²)b - b² = -1
9b³ - b³ = -1
8b³ = -1
b³ = -1/8
a² = 3(1/2)² <- b = -1/2
a² = 3/4
a = ±√3/2
So the three cube roots of -i are:
a + bi
Using a = 0, b = -1/2
a + bi = (-1/2)i
Using a = ±√3/2,
a + bi = ±√3/2 - (1/2)i
(-1/2)i + [√3/2 - (1/2)i] + [-√3/2 - (1/2)i] =
(-1/2)i + √3/2 - (1/2)i - √3/2 - (1/2)i = 0
----
Edwin
|
|
|