Question 1076735: What is the number of distinct solution of the equation 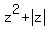 = =  ? ?
Answer by ikleyn(52784)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
What is the number of distinct solution of the equation 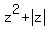 = =  ? ?
~~~~~~~~~~~~~~~~~~~~~
Let us write the number z in Trigonometry form: z = 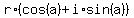 .
Then .
Then  = = 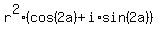 , and your equation is , and your equation is
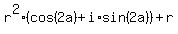 = =  , or, which is the same, , or, which is the same,
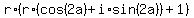 = 0.
The last equation deploys in two independent equations
1) r = 0, which means simply z = 0.
2) (r*(cos(2a) + i*sin(2a)) + 1 = 0, which is the same as
r*(cos(2a) + i*sin(2a) = -1.
The last equation implies
r = 1, cos(2a) = -1 and sin(2a) = 0, which, in turn, implies
r = 1 and {2a = pi OR 2a = = 0.
The last equation deploys in two independent equations
1) r = 0, which means simply z = 0.
2) (r*(cos(2a) + i*sin(2a)) + 1 = 0, which is the same as
r*(cos(2a) + i*sin(2a) = -1.
The last equation implies
r = 1, cos(2a) = -1 and sin(2a) = 0, which, in turn, implies
r = 1 and {2a = pi OR 2a =  }.
It means that the solutions are
a) r = 1, a = }.
It means that the solutions are
a) r = 1, a =  , OR/AND
b) r = 1, a = , OR/AND
b) r = 1, a =  .
In the rectangular form these solutions are z = i OR/AND z = -i.
Answer. The original equation has three solutions: z = 0; z = i, and z = -i. .
In the rectangular form these solutions are z = i OR/AND z = -i.
Answer. The original equation has three solutions: z = 0; z = i, and z = -i.
There is a bunch of lessons on complex numbers
- Complex numbers and arithmetical operations on them
- Complex plane
- Addition and subtraction of complex numbers in complex plane
- Multiplication and division of complex numbers in complex plane
- Raising a complex number to an integer power
- How to take a root of a complex number
- Solution of the quadratic equation with real coefficients on complex domain
- Solved problems on taking roots of complex numbers
- Solved problems on arithmetic operations on complex numbers
- Miscellaneous problems on complex numbers
- Advanced problem on complex numbers
- A curious example of an equation in complex numbers which HAS NO a solution
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Complex numbers".
|
|
|