I assume that by log( ) you mean loge( ) and not
log10( ) as most people in the US mean by log( ).
When we want to indicate loge we write ln( ). If
you meant log10 then tell me in the thank-you note
form below and I'll get back to you.
Use Euler's equation:
,
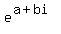
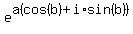Substitute ln(1+i) for a+bi on the left
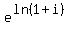
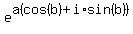
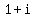
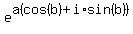eq. 1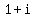 
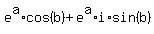Set the real part on the left side of eq. 1
equal to the real part on the right of eq. 1:
eq. 2 
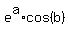Set the imaginary part on the left side of eq. 1
equal to the imaginary part on the right of eq. 1:
eq. 3 
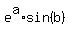Divide equals by equals, that is, divide both side
of eq. 2 by both sides of eq. 1
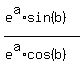
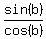
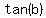The tangent is positive in QI and QIII so
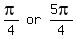However in eq. 3
,
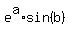the left side is positive, and ea is positive,
so we can discard the QIII answer.
Substitute in eq. 3, using 
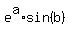
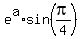
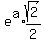
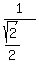
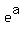
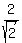
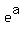
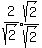
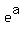
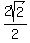
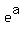
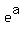Square both sides to eliminate the square root:
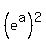
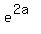Take ln of both sides:
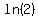
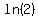
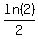
So the solution is
Edwin
