SOLUTION: Convert the integral: <img src="https://i.imgsafe.org/d408b005e9.png"> to polar coordinates and evaluate it.

This double integral is over the unit circle, from the
lower unit semicircle  to the upper unit 
semicircle , so we convert, using , 
and we get:



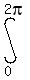
The radius r goes from the origin (the pole) where r is 0
out to the circumference of the unit circle, where r is 1.  
Then the angle q goes around from 0 to 2p . 


Use this taken from a table of integral, to save you
from having to integrate it by parts:



to complete the evaluation.  If you have trouble, tell
me in the thank-you note form below and I'll get back
to you by email.

Edwin