Question 1041293: True or False.
If a sequence is convergent, then the series is convergent. If true, explain why. If false, explain why or provide a counterexample.
Found 2 solutions by ikleyn, rothauserc:
Answer by ikleyn(52788)   (Show Source):
You can put this solution on YOUR website! .
True or False.
If a sequence is convergent, then the series is convergent. If true, explain why. If false, explain why or provide a counterexample.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~`
In mathematics, a series is, informally speaking, the sum of the terms of an infinite sequence.
(Wikipedia, this article.)
False.
Classic counter-example is the harmonic sequence
 ,  ,  , . . . ,  , . . .
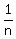The sequence is converged (to zero), but the series is divergent.
Answer by rothauserc(4718)  (Show Source):
|
|
|
