SOLUTION: 1. Create two different rational polynomial expressions with the following constraints: •one expression is undefined when x = 4, •the other is undefined when x = ‒2 or 0.

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson  -> Lesson -> SOLUTION: 1. Create two different rational polynomial expressions with the following constraints: •one expression is undefined when x = 4, •the other is undefined when x = ‒2 or 0.      Log On


   

Question 1032246: 1. Create two different rational polynomial expressions with the following constraints:
•one expression is undefined when x = 4,
•the other is undefined when x = ‒2 or 0.
Then, rewrite both as equivalent expressions, with a common denominator.

2. The expression G over H is multiplied with another rational expression, and the product is 2. What is the other rational expression?
(Note: Please show all work so that I can understand your logic. Thank you.)
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
1.
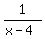1%2F%28x-4%29 is a rational polynomial expression,
with the polynomial 1 as the numerator,
and the polynomial x-4 as the denominator.
It is undefined when x+=+4 .
For those having qualms about calling 1 a polynomial,
we could use a fancier denominator, and write something like
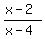%28x-2%29%2F%28x-4%29 (probably a safer choice),
or even 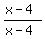%28x-4%29%2F%28x-4%29 (which is not equivalent to 1 , unless you specify "except for x=4 ", so you cannot simplify).

1%2F%28x%5E2%2B2x%29=1%2F%28x%28x%2B2%29%29 is a rational polynomial expression,
with the polynomial 1 as the numerator,
and the polynomial x%5E2%2B2x as the denominator.
It is undefined when x=-2 , and when x=0 .
For those having qualms about calling 1 a polynomial,
we could use a fancier denominator, and write something like
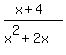%28x%2B4%29%2F%28x%5E2%2B2x%29 .

For a common denominator,
we need to include in that common denominator all the factors of the two denominators.
So, the common denominator would be
x%28x%2B2%29%28x-4%29=x%28x%5E2-2x-8%29=x%5E3-2x%5E2-8x .
To get equivalent rational expression, we need to multiply numerator and denominator times the same factor(s).
So,
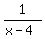1%2F%28x-4%29 is equivalent to x%28x%2B2%29%2F%28x%28x%2B2%29%28x-4%29%29=%28x%5E2%2B2x%29%2F%28x%5E3-2x%5E2-8x%29 .
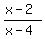%28x-2%29%2F%28x-4%29 is equivalent to .
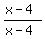%28x-4%29%2F%28x-4%29 is equivalent to .
1%2F%28x%5E2%2B2x%29=1%2F%28x%28x%2B2%29%29 is equivalent to %28x-4%29%2F%28x%28x%2B2%29%28x-4%29%29=%28x-4%29%2F%28x%5E3-2x%5E2-8x%29 .
%28x%2B4%29%2F%28x%5E2%2B2x%29=%28x%2B4%29%2F%28x%28x%2B2%29%29 is equivalent to %28x%2B4%29%28x-4%29%2F%28x%28x%2B2%29%28x-4%29%29=%28x%5E2-16%29%2F%28x%5E3-2x%5E2-8x%29 .

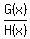2. IF G%28x%29%2FH%28x%29 is an expression defined for all values of x ,
which means that H%28x%29=0 has no real solution, AND
IF G%28x%29=0 has no real solution either,
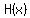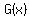H%28x%29 and G%28x%29 are "safe" to use as denominators.
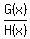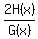Then, multiplying G%28x%29%2FH%28x%29 times 2H%28x%29%2FG%28x%29 will yield