Solved problems on taking roots of complex numbers
In this lesson you will find solved typical basic problems on taking roots of complex numbers.
The solutions are based on a general theory and the formulas of the lesson How to take a root of a complex number in this site.
Problem 1
What are the three cube roots of "i"? Express the roots in rectangular form.
Solution
The trigonometric form of the complex number "i" is cos(90°) + i*sin(90°).
The modulus of "i" is 1, the argument is 90° =  .
According to the general theory, there are three complex cube roots of "i". They have the modulus of
.
According to the general theory, there are three complex cube roots of "i". They have the modulus of  = 1.
The first cube root has the argument of 30° =
= 1.
The first cube root has the argument of 30° =  , one third of the argument of "i".
Each next cube root has the argument in
, one third of the argument of "i".
Each next cube root has the argument in 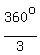 = 120° =
= 120° =  more than the previous one.
Thus the tree complex roots are
1)
more than the previous one.
Thus the tree complex roots are
1) 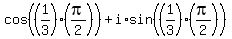 =
=  = cos(30°) + i*sin(30°) =
= cos(30°) + i*sin(30°) =  ;
2)
;
2)  = cos(30°+120°) + i*sin(30° + 120°) = cos(150°) + i*sin(150°) =
= cos(30°+120°) + i*sin(30° + 120°) = cos(150°) + i*sin(150°) = 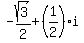 ;
3)
;
3) 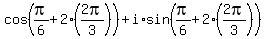 = cos(30°+240°) + i*sin(30° + 240°) = cos(270°) + i*sin(270°) =
= cos(30°+240°) + i*sin(30° + 240°) = cos(270°) + i*sin(270°) = 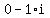 =
= 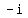 .
.
Problem 2
What are the cube roots of 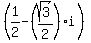 in complex domain?
in complex domain?
Solution
The trigonometric form of the number 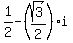 is cos(300°) + i*sin(300°).
The modulus of the number is 1, the argument is 300° =
is cos(300°) + i*sin(300°).
The modulus of the number is 1, the argument is 300° =  .
According to the general theory, there are three complex cube roots of "i". They have the modulus of
.
According to the general theory, there are three complex cube roots of "i". They have the modulus of  = 1.
The first cube root has the argument of 100° =
= 1.
The first cube root has the argument of 100° = 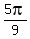 , one third of the argument of the original number.
Each next cube root has the argument in
, one third of the argument of the original number.
Each next cube root has the argument in 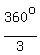 = 120° =
= 120° =  more than the previous one.
Thus the tree complex roots are
1) cos(100°) + i*sin(100°)
2) cos(100°+120°) + i*sin(100°+120°) = cos(220°) + i*sin(220°)
3) cos(100° + 240°) + i*sin(100°+240°) = cos(340°) + i*sin(340°)
more than the previous one.
Thus the tree complex roots are
1) cos(100°) + i*sin(100°)
2) cos(100°+120°) + i*sin(100°+120°) = cos(220°) + i*sin(220°)
3) cos(100° + 240°) + i*sin(100°+240°) = cos(340°) + i*sin(340°)
Problem 3
Determine the fourth roots of -16 in complex domain.
Solution
In the complex plane, -16 = 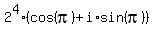 .
The modulus of -16 is
.
The modulus of -16 is 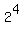 , the argument is 180° =
, the argument is 180° =  .
According to the general theory, there are four complex fourth roots of the number -16. They have the modulus of
.
According to the general theory, there are four complex fourth roots of the number -16. They have the modulus of 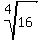 = 2.
The first fourth root has the argument of 45° =
= 2.
The first fourth root has the argument of 45° =  , one fourth of the argument of -16.
Each next fourth root has the argument in
, one fourth of the argument of -16.
Each next fourth root has the argument in  = 90° =
= 90° =  more than the previous one.
Thus the four complex roots are
1)
more than the previous one.
Thus the four complex roots are
1)  =
= 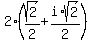 =
= 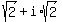 ;
2)
;
2) 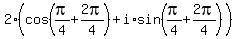 =
=  =
= 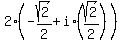 =
= 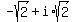 ;
3)
;
3) 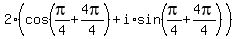 =
= 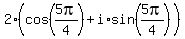 =
= 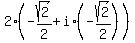 =
= 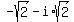 ;
4)
;
4) 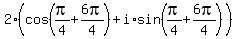 =
=  =
= 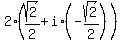 =
= 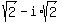 .
Answer. The four values of fourth root of -16 are
.
Answer. The four values of fourth root of -16 are 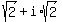 ,
, 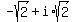 ,
, 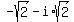 and
and 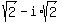 .
.
Problem 4
Find complex roots of degree 4 of -256 in complex domain.
Solution
In the complex plane, -256 = 256*(cos(180°) + i*sin(180°)) = 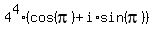 .
The modulus of -256 is
.
The modulus of -256 is 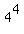 , the argument is 180° =
, the argument is 180° =  .
According to the general theory, there are four complex fourth roots of the number -256. They have the modulus of
.
According to the general theory, there are four complex fourth roots of the number -256. They have the modulus of 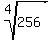 = 4.
The first fourth root has the argument of 45° =
= 4.
The first fourth root has the argument of 45° =  , one fourth of the argument of -256.
Each next fourth root has the argument in
, one fourth of the argument of -256.
Each next fourth root has the argument in  = 90° =
= 90° =  more than the previous one.
Thus the four complex roots are
1) 4(cos(45°) + i*sin(45°)) =
more than the previous one.
Thus the four complex roots are
1) 4(cos(45°) + i*sin(45°)) = 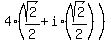 =
=  ;
2) 4(cos(45°+90°) + i*sin(45°+90°)) = 4(cos(135°) + i*sin(135°)) =
;
2) 4(cos(45°+90°) + i*sin(45°+90°)) = 4(cos(135°) + i*sin(135°)) = 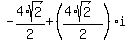 =
= 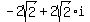 ;
3) 4(cos(45°+180°) + i*sin(45°+180°)) = 4(cos(225°) + i*sin(225°)) =
;
3) 4(cos(45°+180°) + i*sin(45°+180°)) = 4(cos(225°) + i*sin(225°)) = 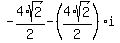 =
=  ;
4) 4(cos(45°+270°) + i*sin(45°+270°)) = 4(cos(315°) + i*sin(315°)) =
;
4) 4(cos(45°+270°) + i*sin(45°+270°)) = 4(cos(315°) + i*sin(315°)) = 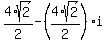 =
=  .
.
Problem 5
What are the 5th roots of 1 in complex domain?
Solution
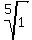 has 5 values in complex domain.
1) 1 (= cos(0°) + i*sin(0°) ),
2) cos(72°) + i*sin(72°),
3) cos(144°) + i*sin(144°),
4) cos(216°) + i*sin(216°),
5) cos(288°) + i*sin(288°).
has 5 values in complex domain.
1) 1 (= cos(0°) + i*sin(0°) ),
2) cos(72°) + i*sin(72°),
3) cos(144°) + i*sin(144°),
4) cos(216°) + i*sin(216°),
5) cos(288°) + i*sin(288°).
Problem 6
What are the fifth roots of -32i?
Solution
Notice that -32i =  .
Therefore, due to DeMoivre formulas, the 5-th degree roots of -32i are
(1) 2cis(54°); ( notice that 54° =
.
Therefore, due to DeMoivre formulas, the 5-th degree roots of -32i are
(1) 2cis(54°); ( notice that 54° = 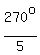 );
(2)
);
(2)  = = 2cis(54° + 72°) = 2cis(126°); ( Notice that 72° =
= = 2cis(54° + 72°) = 2cis(126°); ( Notice that 72° = 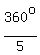 )
(3)
)
(3) 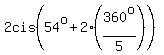 = 2cis(54° + 2*72°) = 2cis(198°);
(4)
= 2cis(54° + 2*72°) = 2cis(198°);
(4) 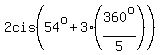 = 2cis(54° + 3*72°) = 2cis(270°);
(5)
= 2cis(54° + 3*72°) = 2cis(270°);
(5) 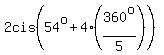 = 2cis(54° + 4*72°) = 2cis(342°).
= 2cis(54° + 4*72°) = 2cis(342°).
Problem 7
Find the sixth roots of 64 in complex domain.
Solution
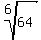 has 6 values in complex domain.
1) 2*(cos(0°) + i*sin(0°)) = 2,
2) 2*(cos(60) + i*sin(60°)) =
has 6 values in complex domain.
1) 2*(cos(0°) + i*sin(0°)) = 2,
2) 2*(cos(60) + i*sin(60°)) = 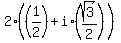 =
= 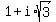 ,
3) 2*(cos(120°) + i*sin(120°)) =
,
3) 2*(cos(120°) + i*sin(120°)) = 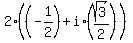 =
= 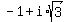 ,
4) 2*(cos(180°) + i*sin(180°)) = -2,
5) 2*(cos(240°) + i*sin(240°)) =
,
4) 2*(cos(180°) + i*sin(180°)) = -2,
5) 2*(cos(240°) + i*sin(240°)) =  =
= 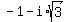 ,
6) 2*(cos(300°) + i*sin(300°)) =
,
6) 2*(cos(300°) + i*sin(300°)) =  =
= 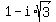 .
.
My lessons on complex numbers in this site are
- Complex numbers and arithmetic operations on them
- Complex plane
- Addition and subtraction of complex numbers in complex plane
- Multiplication and division of complex numbers in complex plane
- Raising a complex number to an integer power
- How to take a root of a complex number
- Solution of the quadratic equation with real coefficients on complex domain
- How to take a square root of a complex number
- Solution of the quadratic equation with complex coefficients on complex domain
- Solved problems on taking roots of complex numbers (this lesson)
- Solved problems on arithmetic operations on complex numbers
- Solved problem on taking square root of complex number
- Solving polynomial equations in complex domain
- Miscellaneous problems on complex numbers
- Advanced problems on complex numbers
- Solved problems on de'Moivre formula
- Proving identities using complex numbers
- Calculating the sum 1*sin(1°) + 2*sin(2°) + 3*sin(3°) + . . . + 180*sin(180°)
- A curious example of an equation in complex numbers which HAS NO a solution
- Solving non-standard equations in complex numbers
- Upper level problem on complex numbers
- Determine locus of points using complex numbers
- Joke problems on complex numbers
- OVERVIEW of lessons on complex numbers
Use this file/link ALGEBRA-II - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-II.

