Can someone also tell me What are (a) the x-intercepts,
(b) the y-intercepts and (c) the foci of the ellipse
(a)_________
(b)_________
(c)_________
Principles you need to learn about the two forms of ellipses.
What is important at first is to observe whether the number
underneath the x² is greater than or less than the number
undernesth the y². The larger of these is always a² amd the
smaller one is always b².
Rule 1.
where 
represents an ellipse that looks like this (
without the pointy thingy.
x-intercepts (a,0) and (-a,0)
y-intercepts (0,b) and (0,-b)
Now to find the foci, first you must
calculate c by the formula
= ±
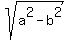for the x-values of the foci.
So the foci are (-c,0) and (c,0).
-------------------------------------
Rule 2.
where
represents an ellipse that is shaped like a zero 0
x-intercepts (b,0) and (-b,0)
y-intercepts (0,a) and (0,-a)
Now to find the foci, first you must
calculate c by the formula
= ±
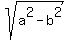for the x-values of the foci.
So the foci are (0,c) and (0,-c).
-------------------------------------
Yours here is the second case since the number
under the y² is greater than the number under
the x²:
so we use rule 2.
so 
so 
since 
represents an ellipse that is shaped like a zero 0
x-intercepts (5,0) and (-5,0)
y-intercepts (0,6) and (0,-6)
Now to find the foci, first you must
calculate c by the formula
= ±
= ±
= ±
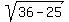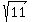or about ±3.3
for the x-values of the foci.
So the foci are (0,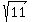) and (0,
),
or about (0,3.3) and (0,-3.3)
Here's the graph. The foci are marked with little short lines:
Edwin
