SOLUTION: The sum of two complex number is 4 and their product is 13. What are the two complex numbers? (a+bi)(c+di) = 13

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: The sum of two complex number is 4 and their product is 13. What are the two complex numbers? (a+bi)(c+di) = 13      Log On


   

Question 913204: The sum of two complex number is 4 and their product is 13. What are the two complex numbers?
(a+bi)(c+di) = 13
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
a%2Bbi%2Bc%2Bdi=4
a%2Bc%2B%28b%2Bd%29i=4
a%2Bc=4 and b%2Bd=0
highlight_green%28b=-d%29

%28a%2Bbi%29%28c%2Bdi%29=13
ac-bd%2B%28bc%2Bad%29i=13
ac-bd=13 and bc%2Bad=0

Substituting for b into these last two equations
ac-%28-d%29d=13
ac%2Bd%5E2=13
and
%28-d%29c%2Bad=0
-cd%2Bad=0
and summarizing the THREE equations which use just variables a,c,d is
highlight_green%28system%28a%2Bc=4%2Cac%2Bd%5E2=13%2C-cd%2Bad=0%29%29

The last equation in the summary of the three-equation system equivalently gives
d%28a-c%29=0

Looking at the first equation of that system and the last equation and assuming 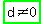highlight_green%28d%3C%3E0%29, then
system%28a%2Bc=4%2C%28a-c%29d=0%29
with the assumption about d allows to have the system:
system%28a%2Bc=4%2Ca-c=0%29

Find through adding first of those to the last of those,
2a=4
highlight%28a=2%29
and then
a%2Bc=4
2%2Bc=4
highlight%28c=2%29

Return to the two equation which came from the product 13.
-
ac-bd=13
2%2A2-bd=13
-bd=13-4
bd=-9----coming back to this after other steps...
-
-bc%2Bad=0, also from the product 13 situation
2%2Ab%2B2%2Ad=0, because we know a and c
2%28b%2Bd%29=0
b%2Bd=0
-
Again bd=-9
bd=%28-d%29d=-9
d%5E2=9
highlight%28d=3%29----- or negative 3 as well.
-
Because we found b=-d
-b=d
-b=3
highlight%28b=-3%29

The variables a, b, c, and d, have now been solved for.
ANSWER: The two complex numbers are 2-3i and 2+3i.
b=-d----which we can soon use in substitution.