We will use
1.  ,
2.
,
2.  ,
3.
,
3.  ,
4.
,
4.  ,
5.
,
5.  ----------------------------------------------
----------------------------------------------
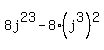 We multiply exponents
We multiply exponents
 We factor out 8
We factor out 8
 Break odd power of j into even power times j:
Write even power as power of jē:
Break odd power of j into even power times j:
Write even power as power of jē:
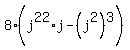 Write even power as power of jē
Substitute -1 for jē:
Write even power as power of jē
Substitute -1 for jē:
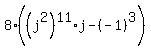 Substitute -1 for jē:
Use
Substitute -1 for jē:
Use 
 Use
Use  Write -(-1) as +1
Write -(-1) as +1
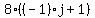 Write (-1)*j as -j
Write (-1)*j as -j
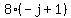 Distribute 8
Distribute 8
 Write j-term second:
Write j-term second:
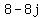 Edwin
Edwin