SOLUTION: Determine which function(s) below have an inverse f^(-1). Can you please explain to me why? (I) f(x)=x^2-2x (II) f(x)=1/x (III) f(x)=cos x (IV)

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: Determine which function(s) below have an inverse f^(-1). Can you please explain to me why? (I) f(x)=x^2-2x (II) f(x)=1/x (III) f(x)=cos x (IV)      Log On


   

Question 805752: Determine which function(s) below have an inverse f^(-1). Can you please explain to me why?
(I) f(x)=x^2-2x (II) f(x)=1/x (III) f(x)=cos x (IV) f(x)=sin x,-π/2≤x≤π/2
(A) I & II
(B) I, II, & III
(C) II, III, & IV
(D) II & IV
(E) none of the above
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
A relation between x and y establishes y as a function of x if for each x we find no more that one y paired to that x.
It could be that y is a function of x that happens to assign the same value of y to more than one x.
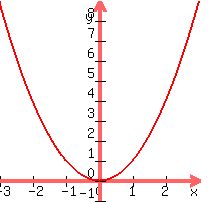
y=x%5E2 is an example. graph%28200%2C200%2C-3%2C3%2C-1%2C9%2Cx%5E2%29
Each x has one and only one x%5E2,
but the same y value can be the y for more than one x,
for example y=4 is the y for x=2 and for x=-2.
In that case, we cannot reverse the function and sat that x is established as a function of y, because for y=4 we find two corresponding values of x.
If there is just one x (or less) for each y, then we can solve for x and find the reverse function.

(I) f%28x%29=x%5E2-2x graph%28200%2C200%2C-2%2C4%2C-2%2C8%2Cx%5E2-2x%29
f%280%29=0=f%282%29 so x=0 and x=2 have the same y=0 ----> There is no inverse function
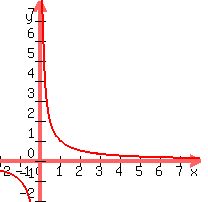
(II) f%28x%29=1%2Fx can be written as y=1%2Fx graph%28200%2C200%2C-2%2C8%2C-2%2C8%2C1%2Fx%29
Exchanging the places of the variables we get x=1%2Fy --> y=1%2Fx
So y=1%2Fx or g%28x%29=1%2Fx%29 is the inverse function of f%28x%29=1%2Fx
That function has an inverse, and is its own inverse.
(III) 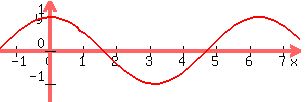f%28x%29=cos+x graph%28300%2C100%2C-1.5%2C7.5%2C-1.5%2C1.5%2Ccos%28x%29%29
We know that cosine is a periodic function with period 2pi so the of y=f%28x%29=cos%28x%29 repeat at 2pi intervals so that cos%280%291=cos%282pi%29=cos%284pi%29%22=+....%22 so we would not know what value of x to assign to y=1.
f%28x%29=cos+x does not have an inverse function
(IV) f%28x%29=sin%28x%29, -pi%2F2%3C=x%3C=pi%2F2 has a restricted range.
f%28-pi%2F2%29=-1 and as x increases f%28x%29=sin+x increases, all the way to f%28pi%2F2%29=sin+%28pi%2F2%29=1 , without repeating any values.
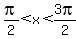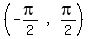For pi%2F2%3Cx%3C3pi%2F2 the values of sin%28x%29 decrease from 1 all the way to -1, repeating values already found for sin%28x%29 in the %28matrix%281%2C3%2C+-pi%2F2+%2C%22%2C%22%2C+pi%2F2%29+%29 interval.
However, with f%28x%29 defined as f%28x%29=sin%28x%29 only in the restricted domain -pi%2F2%3C=x%3C=pi%2F2,
each x corresponds to one and only one y, and vice versa.
The function has an inverse.

So the answer is highlight%28%28D%29%29 II and IV only