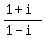 The denominator is 1-i. Let's form the conjugate
of the denominator:
The conjugate of the denominator is formed by
Leaving the sign of the real part, 1, and
changing the sign of the imaginary part i, and
getting 1+i.
Now put 1+i over itself, like this
The denominator is 1-i. Let's form the conjugate
of the denominator:
The conjugate of the denominator is formed by
Leaving the sign of the real part, 1, and
changing the sign of the imaginary part i, and
getting 1+i.
Now put 1+i over itself, like this 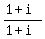 which just equals to 1, and therefore we can multiply
it by the original fraction without changing the
value, like this:
which just equals to 1, and therefore we can multiply
it by the original fraction without changing the
value, like this:
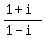

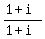 Put parentheses around each factor:
Put parentheses around each factor:


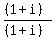 Indicate the multiplication of the two fractions:
Indicate the multiplication of the two fractions:
 Multiply out the top and bottom using "FOIL":
Multiply out the top and bottom using "FOIL":
 Combine terms. The +i and the -i cancel in the
bottom
Combine terms. The +i and the -i cancel in the
bottom
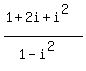 Now we replace each iČ by (-1)
Now we replace each iČ by (-1)
 Simplify:
Simplify:
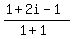

 i
The answer is just simply "i".
Edwin
i
The answer is just simply "i".
Edwin