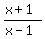 +
+  < -1
Get 0 on the right by adding 1 to both sides:
< -1
Get 0 on the right by adding 1 to both sides:
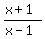 +
+  + 1 < 0
Th LCD is (x-1)(1+x).
+ 1 < 0
Th LCD is (x-1)(1+x).
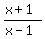 ·
·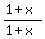 +
+  ·
·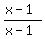 + 1·
+ 1·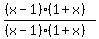 < 0
< 0
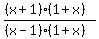 +
+ 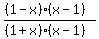 +
+ 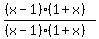 < 0
Multiply out the tops but not the bottoms:
< 0
Multiply out the tops but not the bottoms:
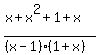 +
+ 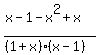 +
+ 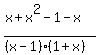 < 0
< 0
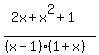 +
+ 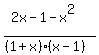 +
+ 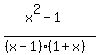 < 0
Write the sum of the numerators over the LCD:
< 0
Write the sum of the numerators over the LCD:
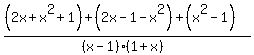 < 0
Take away the parentheses on top:
< 0
Take away the parentheses on top:
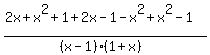 < 0
< 0
 < 0
We find the critical numbers by setting the numerator and
the denominator = 0 and solving:
Numerator = 0
x² + 4x - 1 = 0
That does not factor so we must use the quadratic formula:
< 0
We find the critical numbers by setting the numerator and
the denominator = 0 and solving:
Numerator = 0
x² + 4x - 1 = 0
That does not factor so we must use the quadratic formula:




 Fcator out 2 on the top
Fcator out 2 on the top



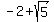 is approximately 0.24 and
is approximately 0.24 and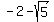 is approximately -4.24
That's two of the critical numbers.
Set denominator = 0
(x - 1)(1 + x) = 0
x - 1 = 0; 1 + x = 0
x = 1; x = -1
So the four critical numbers are
is approximately -4.24
That's two of the critical numbers.
Set denominator = 0
(x - 1)(1 + x) = 0
x - 1 = 0; 1 + x = 0
x = 1; x = -1
So the four critical numbers are
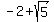 which is approximately 0.24
which is approximately 0.24
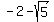 which is approximately -4.24
1
-1
We put those in order smallest to largest:
which is approximately -4.24
1
-1
We put those in order smallest to largest:
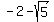 which is approximately -4.24
-1
which is approximately -4.24
-1
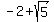 which is approximately 0.24
1
The possible solution intervals are the intervals between and beyond
the critical numbers. None of the critical numbers are solutions, since
the inequality is < and not < so all the possible intervals are
open. They are:
which is approximately 0.24
1
The possible solution intervals are the intervals between and beyond
the critical numbers. None of the critical numbers are solutions, since
the inequality is < and not < so all the possible intervals are
open. They are:
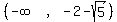
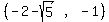
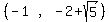
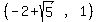
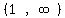 We pick a test value in each interval:
We pick a test value in each interval:
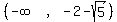 , pick test value -5
, pick test value -5
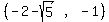 , pick test value -2
, pick test value -2
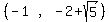 , pick test value 0
, pick test value 0
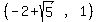 , pick test value .5
, pick test value .5
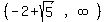 2
We substitute each test value into
2
We substitute each test value into
 < 0
Substituting test value -5
< 0
Substituting test value -5
 < 0
< 0
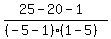 < 0
< 0
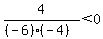 < 0
< 0
 < 0
That is false so
< 0
That is false so 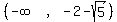 is not part of the solution
Substituting test value -2
is not part of the solution
Substituting test value -2
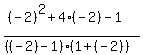 < 0
< 0
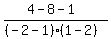 < 0
< 0
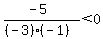 < 0
< 0
 < 0
That is true so
< 0
That is true so 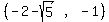 is part of the solution
Substituting test value 0
is part of the solution
Substituting test value 0
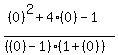 < 0
< 0
 < 0
< 0
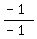 < 0
1 < 0
That is false so
< 0
1 < 0
That is false so 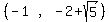 is not part of the solution
Substituting test value .5
is not part of the solution
Substituting test value .5
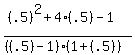 < 0
< 0
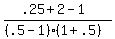 < 0
< 0
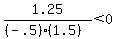 < 0
< 0
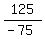 < 0
< 0
 < 0
That is true so
< 0
That is true so 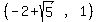 ,
is part of the solution
Substituting test value 2
,
is part of the solution
Substituting test value 2
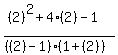 < 0
< 0
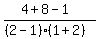 < 0
< 0
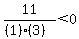 < 0
That is false so
< 0
That is false so 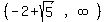 is not part of the solution.
So the solution is
is not part of the solution.
So the solution is
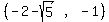 ⋃
⋃ 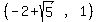 Edwin
Edwin