x5-3x4-8x3-8x2-9x-5=0
The possible rational zeros are ± the factors of 5,
so they are ±1, and ±5
We try the easiest one x=1
1|1 -3 -8 -8 -9 -5
| 1 -2 -10 -18 -27
1 -2 -10 -18 -27 -32
No that gives remaider -32, not 0, so 1 is not a solution
We try the next easiest one x=-1
-1|1 -3 -8 -8 -9 -5
| -1 4 4 4 5
1 -4 -4 -4 -5 0
That gives remaider 0, so -1 is a solution and so we have
factored the polynomial on the left as:
(x + 1)(x4 - 4x³ - 4x² - 4x - 5) = 0
So now we try to factor that polynomial in the second
parentheses:
It also has the same set of possible solutions, so we try -1
again (there is no use to try 1)
-1|1 -4 -4 -4 -5
| -1 5 -1 5
1 -5 1 -5 0
That gives remaider 0, so -1 is a DOUBLE solution
and so we have further factored the polynomial on the left:
(x + 1)(x + 1)(x³ - 5x² + x - 5) = 0
We can now factor the polynomial in the third parentheses by
grouping:
x³ - 5x² + x - 5
x²(x - 5) + 1(x - 5)
(x - 5)(x² + 1)
So we have now factored the original left side as
(x + 1)(x + 1)(x - 5)(x² + 1) = 0
Now we use the zero-factor principle and set each factor = 0
x + 1 = 0, x + 1 = 0, x - 5 = 0, x² + 1 = 0
x = -1 x = -1 x = 5. x² = -1
x =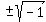 
x = ±i
So the solutions are -1, -1, 5, i, -i.
-1 was a solution twice, so we call it a "double root".
Edwin
