Question 409839: ) Show that if n is a natural number such that 2n-1 is prime, thenn n is a prime. Is the concerse true? Explain?
B) Show that if n is a natural number such that 2n+1 is prime, thenn n is a power of 2. Is the concerse true? Explain?
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! I sure hope you mean  instead of instead of  . In fact I am working on a mathematics project regarding odd perfect numbers, and such a prime in the form . In fact I am working on a mathematics project regarding odd perfect numbers, and such a prime in the form  is important since there is a one-to-one correlation between these primes (called Mersenne primes) and the *even* perfect numbers. is important since there is a one-to-one correlation between these primes (called Mersenne primes) and the *even* perfect numbers.
Suppose that n is not prime, i.e. n = ab for positive integers a and b, where a and b are not equal to 1. Then,  , and this can be factored as , and this can be factored as  (this comes from the geometric series). Since neither factor is 1, then (this comes from the geometric series). Since neither factor is 1, then  can be factored as a product of two integers, hence it is not prime. The contrapositive is true, i.e. if can be factored as a product of two integers, hence it is not prime. The contrapositive is true, i.e. if  is prime, then is prime, then  is prime. The converse is not necessarily true, and we can find counterexamples, such as n = 11, as is prime. The converse is not necessarily true, and we can find counterexamples, such as n = 11, as  . .
Part b is a little tricky, I spent a bit of time on the problem and couldn't come with a full solution. Perhaps you could use an inductive argument, or show that 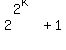 cannot be factored for any k (which might also use induction). cannot be factored for any k (which might also use induction).
|
|
|