SOLUTION: how do i show that 3+2i; 3-2i/13 is multiplicative inverse of one another?

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: how do i show that 3+2i; 3-2i/13 is multiplicative inverse of one another?      Log On


   

Question 265771: how do i show that 3+2i; 3-2i/13 is multiplicative inverse of one another?
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
how do i show that 3+2i; 3-2i/13 is multiplicative inverse of one another

Multiply them together and see if you get 1, the multiplicative identity,
for an answer.

If you get 1, then they are multiplicative inverses of each other.
If you get something other than 1 then they are not.

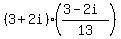%283%2B2i%29%28%283-2i%29%2F13%29

Put the first one over 1:

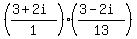%28%283%2B2i%29%2F1%29%28%283-2i%29%2F13%29

Multiply the tops and the bottoms:

%28%283%2B2i%29%283-2i%29%29%2F13

FOIL out the top:

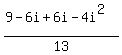
%289-6i%2B6i-4i%5E2%29%2F13

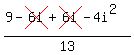
%289-cross%286i%29%2Bcross%286i%29-4i%5E2%29%2F13

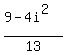%289-4i%5E2%29%2F13

Since i%5E2=-1 replace i%5E2 by -1

%289-4%28-1%29%29%2F13

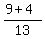
%289%2B4%29%2F13

13%2F13

1

We got 1, the multiplicative identity so that proves 
that they are multiplicative inverses of each other.

Edwin