so the number i is the vector that goes from the
origin to the point (0,1)
That vector has an angle of 
or 90° as we see by the
blue arrow. I'll use this "at" symbol, " @ ", for theta.
So @ = and r = 1.
Trig form for a complex number is
However 
doesn't have to just be identified as because
we may add any multiple of 
to the angle and it will be in
the exact same position. So we use 
where 
represents any integer, positive negative or zero.
So
becomes:
And for both problems:
=
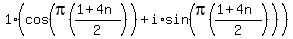Now first we'll take the square root, we raise that to the 
power:
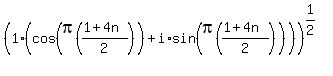Now the rule for simplifying a complex number in trig
form is:
1. Raise the modulus (lenth of vector) to the power
2. Multiply the argument (angle) by the power.
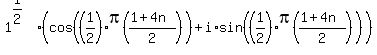which becomes:
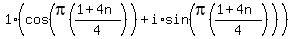or
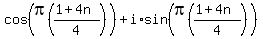Now we let n take on any two consecutive integer values, but
the easiest are n=0 and n=1, so letting n=0:
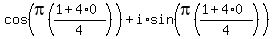
That is this vector:
Now letting n=1:
That is this vector:
So the two square roots of i are
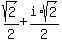and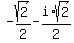 
Putting them both on the same graph:
They form two equally spaced "spokes of a wheel":
-----------------------------------
Now we'll do the cube root of i:
we raise that to the 
power:
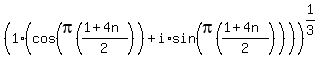Now the rule for simplifying a complex number in trig
form is:
1. Raise the modulus (lenth of vector) to the power
2. Multiply the argument (angle) by the power.
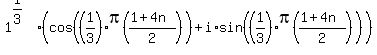which becomes:
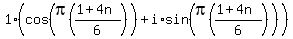or
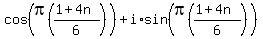Now we let n take on any three consecutive integer values, but
the easiest are n=0, n=1 and n=2, so letting n=0:
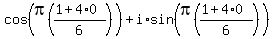
That is this vector:
Now letting n=1:
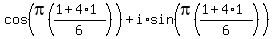
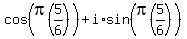
That is this vector:
Now letting n=2:
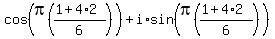
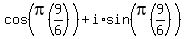
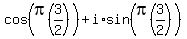
That is this vector:
So the three cube roots of i are
, 
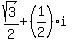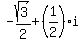, and -i
Putting all three on the same graph:
They form three equally spaced "spokes of a wheel":
Edwin
