Question 1210389: The function f(x) = (1\x) is decreasing on its domain ( true or false)
Found 3 solutions by josgarithmetic, ikleyn, math_tutor2020:
Answer by josgarithmetic(39613)   (Show Source):
Answer by ikleyn(52747)  (Show Source):
You can put this solution on YOUR website! .
First of all, I read this function as f(x) = 1/x,
following to the standard rules commonly accepted in Math.
The domain is the set of all real numbers except of 0 (zero).
Function f(x) = 1/x has two branches: one over the set of positive 'x',
another over the set of negative 'x'.
For each branch separately, function f(x) = 1/x is monotonic in each sub-domain.
Or, more accurately, function f(x) = 1/x is monotonically decreases locally in each sib-domain.
To prove it, take the derivative: it is -  .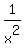
The denominator  is always positive for all 'x' of the domain; so, the derivative is always negative.
You also can convince yourself by making a plot of this function.
For it, go to website https:\\www.desmos.com/calculator/
Print the formula for the function y = 1/x.
You will get the plot instantly.
The plot clearly shows that the function monotonically decreases as 'x' increases in the domain.
So, locally for each branch, the function f(x) = 1/x monotonically decreases.
You have this answer proved formally and demonstrated / illustrated visually.
But we can not say that function f(x) = 1/x is globally decreasing: when 'x' moves
from negative values to positive values, the function 1/x jumps from negative values to positive,
breaking monotonicity.
So, locally this function is monotonically decreasing, but globally it is not monotonic.
//////////////////////////////////////
This problem is an elementary  .
As I explained in my post above, locally and piece-wisely, the function is monotonically decreasing.
But globally, it is NOT monotonic.
It is OBVIOUS: compare these values of the function
x -2 -1 1 2
1/x -0.5 -1 1 0.5
decrease decrease
increase
They show non-monotonic behavior.
Tutor @math_tutor2000 fell into this trap.
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
Answer: true
Explanation
I think you meant to type
f(x) = 1/x
As x gets bigger, i.e. as we move to the right, what happens to y = 1/x?
We can look at a graph to note how it goes downhill throughout its entire domain.
Therefore the answer is true
As x gets bigger, y gets smaller.
As we move to the right the curve goes downhill.
A way to do this without a graph is to plug in a value like x = 2
1/x = 1/2 = 0.50
Then plug in x = 3
1/x = 1/3 = 0.33 approximately
Comparing 0.50 with 0.33 shows that y has gone down, which helps show the function decreases.
Keep in mind that this does not prove it always decreases over the entire domain.
You'll have to use the method mentioned in the next paragraph.
Let's do a formal proof.
Let a > 0 and b > 0.
Since both are positive this means a+b > 0.
Plug in x = a to arrive at 1/a which is also positive.
Plug in x = a+b to arrive at 1/(a+b) which is also positive.
Now to compare 1/a with 1/(a+b)
Assume for now they are equal,
1/a = 1/(a+b)
a+b = a .... cross multiply
b = 0
We arrive at a contradiction since we made b > 0 earlier.
To fix those errors, replace each equal sign with a greater than sign
1/a > 1/(a+b)
a+b > a .... cross multiply
b > 0
Or basically we move through those steps backwards like so
b > 0
a+b > a
1/a > 1/(a+b)
This basically shows that for some input x = a, if we nudge that input to the right a bit to arrive at x = a+b, then we have shown that 1/a is larger than 1/(a+b)
In short we have proven the function is always going downhill no matter where you're on it.
Note that we can follow very similar steps when a < 0 and b > 0, to effectively mirror things over the y axis.
|
|
|
