SOLUTION: The function f(x) = (1\x) is monotonic on its domain ( true or false) ?

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: The function f(x) = (1\x) is monotonic on its domain ( true or false) ?       Log On


   

Question 1210388: The function f(x) = (1\x) is monotonic on its domain ( true or false) ?

Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.
The function f(x) = (1\x) is monotonic on its domain ( true or false) ?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~


        First of all,  I read this function as   f(x) = 1/x,
        following to the standard rules commonly accepted in  Math.


The domain is the set of all real numbers except of 0 (zero).

Function   f(x) = 1/x   has two branches: one over the set of positive  'x',
another over the set of negative  'x'.

For each branch separately,  function   f(x) = 1/x   is monotonic in each sub-domain.


Or, more accurately,  function   f(x) = 1/x   is monotonically decreases locally in each sib-domain.

To prove it,  take the derivative:  it is  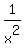 - 1%2Fx%5E2.

The denominator  x%5E2  is always positive for all  'x'  of the domain;   so, the derivative is always negative.

You also can convince yourself by making a plot of this function.

For it,  go to website https:\\www.desmos.com/calculator/

Print the formula for the function  y = 1/x.

You will get the plot instantly.

The plot clearly shows that the function monotonically decreases as  'x'  increases in the domain.

So,  locally for each branch,  the function   f(x) = 1/x   monotonically decreases.
You have this answer proved formally and demonstrated / illustrated visually.


But we can not say that function   f(x) = 1/x   is globally decreasing:   when  'x'   moves
from negative values to positive values,  the function  1/x  jumps from negative values to positive,
breaking monotonicity.

So,  locally this function is monotonically decreasing,  but globally it is not monotonic.


/////////////////////////////////


After reading the post by @math_tutor2020
https://www.algebra.com/algebra/homework/complex/Complex_Numbers.faq.question.1210389.html


            This problem is an elementary  highlight%28highlight%28TRAP%29%29.


As I explained,  locally and piece-wisely,  the function is monotonically decreasing.

But globally,  it is  NOT  monotonic.

It is  OBVIOUS:  compare these values 

    x     -2      -1      1      2   

    1/x   -0.5    -1      1      0.5

           decease        decrease
                   increase

They show non-monotonic behavior.

Tutor  @math_tutor2000  fell into this trap.