Question 1210370: Using the discriminant method, find the range of the function:
y =(x+1)/(sqrt(x² - 5))
Found 2 solutions by mccravyedwin, ikleyn:
Answer by mccravyedwin(409)   (Show Source): (Show Source):
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Using the discriminant method, find the range of the function:
y = (x+1)/(sqrt(x² - 5))
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will solve this problem and will find the range of the given function algebraically,
using the discriminant method.
But for better understanding, I will start from the plot, which I prepared using
the plotting tool DESMOS. This plotting tool is free of charge at this website
http://desmos.com/calculator/
The link to my plot is this https://www.desmos.com/calculator/lhfouvblry
Looking at the function and at the plot, we see that the domain of the function is
x^2-5 > 0, or x <  U x > U x >  (the union of two sets).
In the area x > (the union of two sets).
In the area x >  , when x approaches to , when x approaches to  from the right side, the function
asymptotically goes to infinity.
In the same area, x > from the right side, the function
asymptotically goes to infinity.
In the same area, x >  , when x goes to positive infinity, the function is asymptotically
close to , when x goes to positive infinity, the function is asymptotically
close to 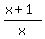 , so, it goes to 1 unit monotonically decreasing.
Hence, the range of the right branch of the function at positive x > , so, it goes to 1 unit monotonically decreasing.
Hence, the range of the right branch of the function at positive x >  is from 1 to infinity,
or ( is from 1 to infinity,
or (  , , ).
In the area x < ).
In the area x <  , when x approaches to , when x approaches to  from the left side, the function
asymptotically goes to negative infinity.
In the same area, x < from the left side, the function
asymptotically goes to negative infinity.
In the same area, x <  , when x goes to negative infinity, the function is asymptotically
close to , when x goes to negative infinity, the function is asymptotically
close to 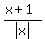 , so, it goes to negative 1 unit, or (-1), monotonically decreasing.
But at x = -3, the value of the function is (-1), as it is easy to check, and then, in the area , so, it goes to negative 1 unit, or (-1), monotonically decreasing.
But at x = -3, the value of the function is (-1), as it is easy to check, and then, in the area
 < x < 3, the function is greater than -1 and tends to -1 from greater values than -1.
Hence, the function has a local maximum somewhere between -3 and < x < 3, the function is greater than -1 and tends to -1 from greater values than -1.
Hence, the function has a local maximum somewhere between -3 and  .
+------------------------------------------------------------------------+
| The major goal of this problem is to determine this local maximum. |
| As we get this local maximum, we will solve the problem completely. |
+----------------------------------------------------------------------=-+
OK. The next part of the solution is the .
+------------------------------------------------------------------------+
| The major goal of this problem is to determine this local maximum. |
| As we get this local maximum, we will solve the problem completely. |
+----------------------------------------------------------------------=-+
OK. The next part of the solution is the  . Let's write . Let's write
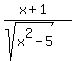 = t, (1)
by introducing new variable 't'.
We want to find maximum value of 't' in the area = t, (1)
by introducing new variable 't'.
We want to find maximum value of 't' in the area  < x < < x <  .
From equation (1), we have
(x+1)^2 = t^2*(x^2-5),
x^2 + 2x + 1 = t^2*x^2 - 5t^2,
(t^2-1)x^2 - 2x - (5t^2+1) = 0. (2)
+---------------------------------------------------------------------+
| The discriminant principle says that the extremal value of 't' |
| in this equation is achieved when the discriminant |
| of this equation is zero. |
| It is the condition that equation (2) has emerging roots in x. |
+---------------------------------------------------------------------+
So, the discriminant of equation (2) is
d = b^2 - 4ac = (-2)^2 + 4*(t^2-1)*((5t^2+1) = 4 + 4(t^2-1)*(5t^2+1).
The equation d = 0 is then
4 + 4(t^2-1)*(5t^2+1) = 0,
or
(t^2-1)*(5t^2+1) = -1. (3)
For simplicity, let's introduce new variable u = t^2.
Then equation (3) takes the form
(u-1)*(5u+1) = -1,
5u^2 - 4u - 1 = -1,
5u^2 - 4u = 0,
u*(5u - 4) = 0.
It has the roots u = 0 and u = .
From equation (1), we have
(x+1)^2 = t^2*(x^2-5),
x^2 + 2x + 1 = t^2*x^2 - 5t^2,
(t^2-1)x^2 - 2x - (5t^2+1) = 0. (2)
+---------------------------------------------------------------------+
| The discriminant principle says that the extremal value of 't' |
| in this equation is achieved when the discriminant |
| of this equation is zero. |
| It is the condition that equation (2) has emerging roots in x. |
+---------------------------------------------------------------------+
So, the discriminant of equation (2) is
d = b^2 - 4ac = (-2)^2 + 4*(t^2-1)*((5t^2+1) = 4 + 4(t^2-1)*(5t^2+1).
The equation d = 0 is then
4 + 4(t^2-1)*(5t^2+1) = 0,
or
(t^2-1)*(5t^2+1) = -1. (3)
For simplicity, let's introduce new variable u = t^2.
Then equation (3) takes the form
(u-1)*(5u+1) = -1,
5u^2 - 4u - 1 = -1,
5u^2 - 4u = 0,
u*(5u - 4) = 0.
It has the roots u = 0 and u =  = 0.8.
The root u = 0 is irrelevant and we reject it.
The root u = 4/5 = 0.8 gives us
t^2 = = 0.8, t = +/- = 0.8.
The root u = 0 is irrelevant and we reject it.
The root u = 4/5 = 0.8 gives us
t^2 = = 0.8, t = +/- 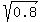 = +/- = +/- 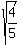 = +/- = +/- 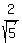 = +/- 0.894427.
The positive value is irrelevant (extraneous), and we reject it.
But the negative value, t = -0.894427 gives us the maximum value of the function y = = +/- 0.894427.
The positive value is irrelevant (extraneous), and we reject it.
But the negative value, t = -0.894427 gives us the maximum value of the function y = 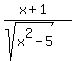 for its left branch over the domain
for its left branch over the domain  < x < -3.
Thus the range of the given function is ( < x < -3.
Thus the range of the given function is (  , ,  ] U ( ] U (  , , ),
the union of two intervals.
It is consistent with my plot, referred above. ),
the union of two intervals.
It is consistent with my plot, referred above.
At this point, the problem is solved completely.
|
|
|