SOLUTION: find the range of f(x) = 1/(sqrt(x + 1) + sqrt(x - 1))

The domain of the given function is the set of real numbers { x >= 1 },
where all square roots are defined.


Both functions,    and    increase monotonically as 'x' increases
frm 1 to infinity.


Hence, function  f(x) = 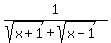  decreases monotonically as 'x' increases 
from 1 to infinity. 


It means that the upper bound of the range of function  f(x) is  f(1) =  =  = .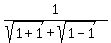


As x goes to infinity, the denominator in the function f(x) definition becomes infinitely great,
so the function f(x) tends to zero, but does not get the value of zero.


Thus the range of function f(x) is  [ , ).    ANSWER