SOLUTION: Describe all solutions to z -3w - 2iw + 4iz = -8 where z and w are complex numbers.

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: Describe all solutions to z -3w - 2iw + 4iz = -8 where z and w are complex numbers.      Log On


   

Question 1209146: Describe all solutions to z -3w - 2iw + 4iz = -8 where z and w are complex numbers.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


z+-3w+-+2iw+%2B+4iz+=+-8

Let z = a+bi
Let w = c+di

%28a%2Bbi%29-3%28c%2Bdi%29-2i%28c%2Bdi%29%2B4i%28a%2Bbi%29=-8

%281%2B4i%29%28a%2Bbi%29-%283%2B2i%29%28c%2Bdi%29=-8

%28a-4b-3c%2B2d%29%2B%284a%2Bb-2c-3d%29i=-8%2B0i

Equating the real and imaginary parts on both sides of the equation....

a-4b-3c%2B2d=-8 and 4a%2Bb-2c-3d=0

That's two equations in 4 unknowns. The best you can do is eliminate one variable to get a single (linear) equation in three unknowns, which will have an infinite number of solutions.

Solving the second equation for b and substituting in the first equation....

b=-4a%2B2c%2B3d

a-4%28-4a%2B2c%2B3d%29-3c%2B2d=-8

a%2B16a-8c-12d-3c%2B2d=-8

17a-11c-10d=-8

That last equation "describes" all the solutions to the given equation.

For one simple solution (undoubtedly the simplest), let b=d=0, making z=a and w=c:

a-3c=-8
4a-2c=0

Solve by elimination:

4a-2c=0
4a-12c=-32
10c=32
c=3.2
a-3%283.2%29=-8
a-9.6=-8
a=1.6

Simplest solution:
z = 1.6+0i
w = 3.2+0i

Answer by ikleyn(52778) About Me  (Show Source):
You can put this solution on YOUR website!
.
Describe all solutions to z -3w - 2iw + 4iz = -8 where z and w are complex numbers.
~~~~~~~~~~~~~~~~~~~~~~~~~ 

Your starting equation is

    z -3w - 2iw + 4iz = -8, 

where z  and  w are complex numbers/variables.


In the equation, collect and combine like terms.  You will get

    (z+4iz) - (3w+2iw) = -8,

    (1+4i)z - (3+2i)w = -8,

    (1+4i)z = -8 + (3+2i)w,

    z = 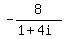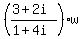-8%2F%281%2B4i%29 + %28%283%2B2i%29%2F%281%2B4i%29%29%2Aw.


Thus, in this case, there are infinitely many possible solutions.
"w"  can be any complex number, and then  "z"  is expressed via  "w"  by this formula.


It is the full description of the solution set.


It is similar to the regular real case, when you are given one linear equation 
for two unknown, and you are asked to describe all possible solutions.


Then (in the regular case) one unknown is a free variable (as "w" in this case), 
while the second unknown is a linear function of the first variable.

Solved.

It is what you need to understand and what they want to get / (to hear) from you as your answer.