SOLUTION: limit (((ln 2))^(x))/(cos ((pi)/4 sin (3 x))) as x \[LongRightArrow] - \[Infinity] = 0 ( T or F )

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: limit (((ln 2))^(x))/(cos ((pi)/4 sin (3 x))) as x \[LongRightArrow] - \[Infinity] = 0 ( T or F )      Log On


   

Question 1208976: limit (((ln 2))^(x))/(cos ((pi)/4 sin (3 x))) as x \[LongRightArrow] - \[Infinity] = 0 ( T or F )
Answer by ikleyn(52761) About Me  (Show Source):
You can put this solution on YOUR website!
.
limit (((ln 2))^(x))/(cos ((pi)/4 sin (3 x))) as x \[LongRightArrow] - \[Infinity] = 0 ( T or F )
~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

I placed (copy-pasted) the given expression into the Math editor, and this Math editor interpreted the expression this way

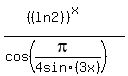    %28%28%28ln+2%29%29%5E%28x%29%29%2F%28cos+%28%28pi%29%2F4+sin+%283+x%29%29%29.


It is what I will use in my following analysis.


             Step 1.


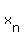Consider a sequence of real numbers  x%5B1%5D, x%5B2%5D, x%5B3%5D, . . . , x%5Bn%5D, . . . which approaches to  pi%2F18  from the left.

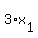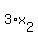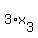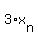Then the sequence of real numbers  3%2Ax%5B1%5D, 3%2Ax%5B2%5D, 3%2Ax%5B3%5D, . . . , 3%2Ax%5Bn%5D, . . . approaches to  pi%2F6  from the left.

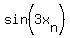Then the sequence of real numbers  sin%283%2Ax%5B1%5D%29, sin%283%2Ax%5B2%5D%29, sin%283%2Ax%5B3%5D%29, . . . , sin%283x%5Bn%5D%29  approaches to  sin%28pi%2F6%29 = 1/2  from the left.

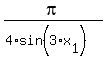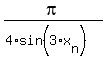Then the sequence of real numbers  pi%2F%284%2Asin%283%2Ax%5B1%5D%29%29, pi%2F%284%2Asin%283%2Ax%5B2%5D%29%29, pi%2F%284%2Asin%283%2Ax%5B3%5D%29%29, . . . , pi%2F%284%2Asin%283%2Ax%5Bn%5D%29%29, . . .  

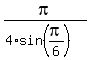         approaches to  pi%2F%284%2Asin%28pi%2F6%29%29 = pi%2F%284%2A%281%2F2%29%29 = pi%2F2  from the left.


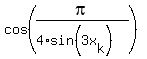Then the sequence of numbers  cos%28pi%2F%284%2Asin%283x%5Bk%5D%29%29%29  approaches to  0 (zero)  from the right.


Thus for this sequence of numbers  x%5Bk%5D,  the numerator approaches to (ln(2))^(pi/18), which is some constant,

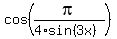while the denominator  cos%28pi%2F%284%2Asin%283x%29%29%29  approaches to zero.


Hence, as the argument x approaches to  pi%2F18  from the left,  
the values of the given expression go to positive infinity.


After that, as the argument x becomes greater than pi%2F18, the expression takes finite values, again.


             Step 2.


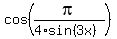The function  cos%28pi%2F%284%2Asin%283x%29%29%29  in the denominator is periodical with the period 2pi%2F3.


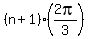It means that the behavior of the given expression, which we detected in part (a), repeats inside each period [n%2A%282pi%2F3%29,%28n%2B1%29%2A%282pi%2F3%29],
for all positive or negative integer numbers "n".


In other words, inside each such period, there is a converging sequence of real numbers, 
for which our expression goes to positive infinity, and after that the expression takes finite values, again.


             Step 3.


It means that as x goes to plus or minus infinity, the given expression HAS NO limit.


ANSWER.  Of the two possible options, T or F, only F is valid.

Solved.


========================


It can be solved in other way, too. 

In my solution above, I considered a sequence of numbers  x%5Bk%5D,  converging to  pi/6  from the left,
and shoved that for such sequence  of arguments the whole function has positive values (going to + infinity).


Similarly, if we consider another sequence of numbers  x%5Bk%5D, converging to pi/6 from the right,
we will get the sequence of the values of the whole function, which all are negative and go to - infinity.



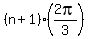Such a behavior repeats at each interval [n%2A%282pi%2F3%29,%28n%2B1%29%2A%282pi%2F3%29], for all positive or negative integer numbers "n".


But the function with such a behavior can not have limits as x goes to +infinity or -infinity.



So, the given function has no limits as x goes to +infinity or -infinity.