.
find : limit ((ln (2)))^(x) \[Times] sec ((pi)/4 sin (3 x)) as x \[LongRightArrow] - \[Infinity]
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The function under the question is
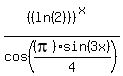 .
This function has periodic denominator. The period of the denominator is
.
This function has periodic denominator. The period of the denominator is  ~
~  ~ 2.09...
The denominator is zero when
~ 2.09...
The denominator is zero when
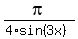 = +/-
= +/-  .
Hence, the whole function has vertical asymptotes at
4*sin(3x) = +/- 2, sin(3x) = +/-
.
Hence, the whole function has vertical asymptotes at
4*sin(3x) = +/- 2, sin(3x) = +/-  ,
3x =
,
3x = 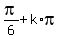 , or 3x =
, or 3x = 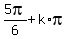 , or 3x =
, or 3x = 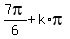 , or 3x =
, or 3x = 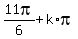 ,
so respectively
x =
,
so respectively
x = 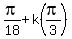 , or x =
, or x = 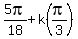 , or x =
, or x = 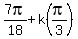 , or x =
, or x =  ,
for all integer k = 0, +/-1, +/-2, . . .
So, placing of asymptotes is quite exotic; but as the argument x approaches
to the asymptote, the function goes to positive infinity or to negative infinity,
with some alternating, and it repeats with each period of the denominator.
See the plot in the Figure below.
,
for all integer k = 0, +/-1, +/-2, . . .
So, placing of asymptotes is quite exotic; but as the argument x approaches
to the asymptote, the function goes to positive infinity or to negative infinity,
with some alternating, and it repeats with each period of the denominator.
See the plot in the Figure below.
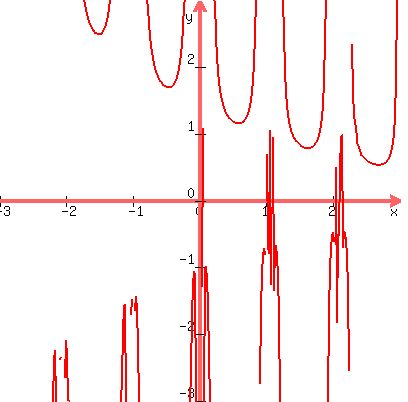 Figure.
Due to this behavior, the whole function has no limit as x goes to plus infinity or to minus infinity.
Figure.
Due to this behavior, the whole function has no limit as x goes to plus infinity or to minus infinity.
Solved.