Question 1207776: How many random ways can a 20-question multiple-choice test be answered, with each question having 4 options?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 1,099,511,627,776
This is roughly 1.0995 trillion
Work Shown
4^20 = 1099511627776
Explanation
Let's say for the sake of simplicity there are 2 questions with 4 options each.
Consider a 4 by 4 table. There are 4*4 = 4^2 = 16 different ways to answer these two questions.
This is because there are 16 inner cells of this table.
Now consider a test with 3 questions. Each has 4 options.
We found earlier that there are 16 ways to answer the first two questions.
Consider a table that has 16 rows and 4 columns.
The row count is how many ways to answer the first two questions, while the columns are the options for the third question.
We have 16*4 = 64 ways to answer these 3 questions
Or put another way 4^3 = 64
This pattern can be continued for as long as you like.
In general, if an exam has n questions with 4 options each, then there will be 4^n different ways to select the options.
In the "work shown" section above, I plugged in the value n = 20.
The massive number 1099511627776 is roughly 1.0995 trillion.
In scientific notation, it's roughly equal to 1.0995 * 10^12
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many random ways can a 20-question multiple-choice test be answered,
with each question having 4 options?
~~~~~~~~~~~~~~~~~~~~~
Imagine that the option are A, B, C, D (i.e., the options are marked by letter A, B, C, and D).
Then one whole answer to 20 multiple choice question is a 20-letters word, written in the alphabet A, B, C, D.
Different answers create different words, and different words correspond to different answers.
So, the problem's question is the same as to ask: how many 20-letters words
do exist in 4-letter alphabet A, B, C, D.
The letters in different positions are independent; in each position, any of 4 letters can be.
So, the ANSWER is: 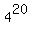 = 1099511627776 different 20-letter words are possible
in the alphabet A, B, C and D.
Hence, = 1099511627776 different 20-letter words are possible
in the alphabet A, B, C and D.
Hence, 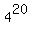 = 1099511627776 different answers are possible in this multiple choice test. = 1099511627776 different answers are possible in this multiple choice test.
Solved.
----------------------
This model using words of the certain length written in some alphabet is useful for solving such problems
on multiple choice tests, and for solving many other combinatorics problems, where there is
a finite number of independent trials with the fixed number of independent outcomes for each trial.
To see many other similar (and different) problems of this kind, look into the lesson
- Combinatoric problems for entities other than permutations and combinations
in this site.
|
|
|