.
Simplify the square root. Write your answer in the form a + bi.
sqrt{(4 + 3i)(3i - 4)}
Do I FOIL the radicand?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Working with radicand, you may do FOIL or you may use shortcut 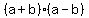 =
=  -
-  .
In any case and in any way, you will get the same value of -25 for the radicand.
So, your first simplification step is
.
In any case and in any way, you will get the same value of -25 for the radicand.
So, your first simplification step is  =
= 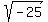 .
+------------------------------------------------------+
| But the most interesting things start from here. |
+------------------------------------------------------+
The fact is that square root of complex number in complex domain ALWAYS has TWO VALUES,
that have opposite signs. Concretely,
.
+------------------------------------------------------+
| But the most interesting things start from here. |
+------------------------------------------------------+
The fact is that square root of complex number in complex domain ALWAYS has TWO VALUES,
that have opposite signs. Concretely,
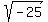 = +/- 5i.
Yes, I did not misspeak:
= +/- 5i.
Yes, I did not misspeak: 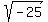 has two values. One value is 5i, another value is -5i.
It is because
has two values. One value is 5i, another value is -5i.
It is because 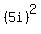 = -25 and
= -25 and 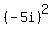 = -25.
In real number domain, there is a selected set of positive numbers;
therefore, for positive numbers we can get agreement that the square root
of positive real number is a positive real number.
But in complex domain, there is no such selected set as positive numbers.
Therefore, the square root ALWAYS has TWO different values in complex domain.
There is only one exclusion from this rule: it is the number 0 (zero), which has only one
value of the square root. All other (non-zero) complex numbers have TWO values
of square root, and these two values have EQUAL RIGHTS to exist as the values of the square root
in complex domain.
Therefore, the right answer to this problem question is that
= -25.
In real number domain, there is a selected set of positive numbers;
therefore, for positive numbers we can get agreement that the square root
of positive real number is a positive real number.
But in complex domain, there is no such selected set as positive numbers.
Therefore, the square root ALWAYS has TWO different values in complex domain.
There is only one exclusion from this rule: it is the number 0 (zero), which has only one
value of the square root. All other (non-zero) complex numbers have TWO values
of square root, and these two values have EQUAL RIGHTS to exist as the values of the square root
in complex domain.
Therefore, the right answer to this problem question is that 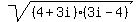 has
two different values, namely, 5i and -5i.
You can write them in the form a+bi: 5i = 0 + 5i;
-5i = 0 - 5i.
The answer in WolframAlpha
https://www.wolframalpha.com/input?i=sqrt%28+%284%2B3i%29%283i-4%29+%29+%3D+5i
stating that
has
two different values, namely, 5i and -5i.
You can write them in the form a+bi: 5i = 0 + 5i;
-5i = 0 - 5i.
The answer in WolframAlpha
https://www.wolframalpha.com/input?i=sqrt%28+%284%2B3i%29%283i-4%29+%29+%3D+5i
stating that 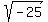 = 5i is INCORRECT in this case, because it is INCOMPLETE.
It gives only one value 5i for
= 5i is INCORRECT in this case, because it is INCOMPLETE.
It gives only one value 5i for 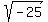 in complex domain,
while there are TWO different values for it, 5i and -5i.
SIMILARLY,
in complex domain,
while there are TWO different values for it, 5i and -5i.
SIMILARLY, 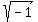 has two values, i and -i.
I will shock you even more, when I'll say that in complex domain,
the n-th root of any non-zero complex number has n different values.
But it is TRUE.
In fact, only those, who professionally know complex numbers and who learned/studied
a full course of complex numbers analysis in combination with abstract algebra
at universities, do understand this fully.
Only those have really NON-SELF-CONTRADICTORY understanding of this subject in their minds
(under the condition that they learned from good professors and from good textbooks).
has two values, i and -i.
I will shock you even more, when I'll say that in complex domain,
the n-th root of any non-zero complex number has n different values.
But it is TRUE.
In fact, only those, who professionally know complex numbers and who learned/studied
a full course of complex numbers analysis in combination with abstract algebra
at universities, do understand this fully.
Only those have really NON-SELF-CONTRADICTORY understanding of this subject in their minds
(under the condition that they learned from good professors and from good textbooks).
///////////////////
So, let me repeat it again, because it is of great importance.
The answer in WolframAlpha
https://www.wolframalpha.com/input?i=sqrt%28+%284%2B3i%29%283i-4%29+%29+%3D+5i
stating that 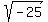 = 5i is INCORRECT in this case, because it is INCOMPLETE.
It gives only one value 5i for
= 5i is INCORRECT in this case, because it is INCOMPLETE.
It gives only one value 5i for 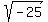 in complex domain,
while there are TWO different values for it, 5i and -5i.
in complex domain,
while there are TWO different values for it, 5i and -5i.
Thus the reference to WolframAlpha in this case " for confirmation " does not work.
WolframAlpha is WRONG in this case.
\\\\\\\\\\\\\\\\\\\\\\\\\
Dear tutor @math_tutor2020, read THIS from Wikipedia
about the roots of degree n of complex numbers
https://en.wikipedia.org/wiki/Nth_root#:~:text=Every%20non%2Dzero%20number%20x,root%20of%200%20is%200.&text=All%20nth%20roots%20of%20rational,of%20integers%20are%20algebraic%20integers.
Read this part, highlighted in the referred text:
Every non-zero number x, real or complex,
has n different complex number nth roots.
It is well known fact after deMoivre, Euler, Riemann . . .
And after reading it, please stop argue with me.
\\\\\\\\\\\\\\\\\\\\\\\\
Regarding notices by @math_tutor2020 about values of square roots.
On real number domain,
- square roots ALWAYS have two values for positive numbers: one positive value and one (opposite) negative value;
- square root has one value for the number of zero;
- square root is not defined for negative numbers.
Sometime (quite often), we want to consider square root functions over real numbers.
Then, to satisfy a vertical line test for functions, we accept an agreement that we consider
only positive values of square root function.
It is critically important for a student to know and to understand, that it is only an AGREEMENT;
that square root ALWAYS has two values due to its nature (when defined).
It is only by agreement we accept that the square root real functions take only positive values.
In complex number domain, square root ALWAYS has two values.
In school course of complex numbers, square root functions are not considered.
In university courses of complex analysis, there are two levels of consideration square root functions
and, generally, n-root functions.
One level, which is basic for all specialties, except of graduate in Math, considers square functions
as two-values and n-root functions as n-values.
Other level, for graduate students in Math, specializing in Topology, Algebraic geometry, number theory,
consider square root functions and n-root functions over Riemannian surfaces,
which makes them 1-valued. But this level uses totally different conceptions and is far from the school level.
It is what (ideally) a person who studies
this great piece of Math should know.
In reality, of 70,000 US school Math teachers, probably, only 70 persons do understand it clearly.
The rest of the teachers do not have clear understanding on the subject and are totally
intimidated by the vertical line test for square root functions.
They themselves are intimidated and intimidate their students, too;
so, in this community, there is NO right understanding of the nature of things.