Question 1194290: Two numbers differ by 8 and their name product is 209. Find the numbers
Found 3 solutions by Boreal, ikleyn, greenestamps:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! x and y
I assume their product is 209
xy=209
x-y=8
x=y+8
so (y+8)*y=209
y^2+8y-209=0
(y+19)(y-11)=209
The numbers are 11 and 19 or -11 and -19
Answer by ikleyn(52756)  (Show Source):
You can put this solution on YOUR website! .
Let x be the number exactly half way between our two numbers.
Then the two numbers are x+4 and x-4; their product is (x+4)*(x-4) = x^2 - 16.
So we have this equation for x
x^2 - 16 = 209
x^2 = 209 + 16 = 225.
Thus x = 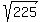 = +/- 15/
The problem has two solutions.
One solution is the pair (15-4,15+4) = (11,19).
Another solution is the pair (-15-4,-15+4) = (-19,-11).
Solved.
Answer by greenestamps(13196)  (Show Source):
You can put this solution on YOUR website!
Notice that, in the formal algebraic solution from @boreal, you have to factor a quadratic expression by finding two numbers whose difference is 8 and whose product is 209.
But that is exactly what the original problem asks you to do -- so that formal algebraic method doesn't help you get any closer to the answer.
If you need a formal algebraic solution, use the nice "trick" shown by tutor @ikleyn. As she says in her response, it is a very useful method applicable to many problems.
But if formal algebra is not required, clearly the fastest way to the answer is to find how the product 209 factors.
209 = 11*19
So the two numbers are 11 and 19.
Then, since the problem allows negative answers, another solution is -11 and -19.
|
|
|
