Question 1181018: Please help me solve this problem
Convert the General Equation 36y2-64x2-128x-144y-2512=0 to Standard form.
Sketch and determine the parts of the Hyperbola.
Parts of Hyperbola:
1. Center
2. Foci
3. Vertices
4. Length of Conjugate Axis B1, B2
5. End Points of Latus Rectum E1, E2, E3, E4
6. Asymptotes
7. Eccentricity
8. Length of LR
9. Length of Conjugate Axis
10. Length of Traverse Axis
Thank you and God bless
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Convert the General Equation
 to Standard form. to Standard form.







 ....both sides divide by ....both sides divide by 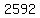
 ...simplify ...simplify


Up-down hyperbola with:
=> , ,  , ,
 , , 
Sketch and determine the parts of the Hyperbola.
Parts of Hyperbola:
1. Center:=> , ,  => center ( => center ( , ,  ) )
2. Foci: 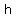 or or 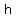
 -> ->
so, foci are at
( , ,  ) or ( ) or ( , , 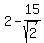 ) )
( , , 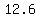 ) or ( ) or ( , , 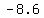 ) )
3. Vertices:( , , 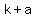 ), and the other is at ( ), and the other is at ( , , 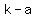 ) )
( , , 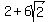 ), ( ), ( , , 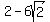 ) )
( , , 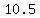 ), ( ), ( , , 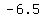 ) )
Co-vertices :
( , ,  ) => ( ) => ( , ,  ) )
( , ,  ) =>( ) =>(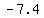 , ,  ) )
4. End Points of Conjugate Axis B1, B2
The co-vertices of a hyperbola are the endpoints of the conjugate axis
B1=( , ,  ) )
B2=(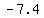 , ,  ) )
distance between: 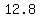
5. End Points of Latus Rectum
take y coordinate of the focus, as a line
foci is at ( , , 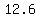 ) or ( ) or ( , , 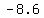 ) )
take  and find intersection with and find intersection with 

 ≈ ≈ 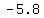
 ≈ ≈ 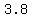
E1= ( 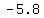 , ,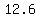 ) )
E2=(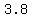 , ,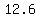 ) )
E3=(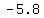 , ,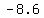 ) )
E4=(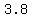 , ,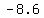 ) )
6. Asymptotes:  , ,
7. Eccentricity:
8. Length of LR: ≈ ≈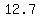
10. Length of Traverse Axis:12sqrt(2) ≈16.97

|
|
|