SOLUTION: Part A: For the function y=sin x , the value of 3pi over 2 is marked. At what point does this cycle end? Part B: For the function y=cos x , the value

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: Part A: For the function y=sin x , the value of 3pi over 2 is marked. At what point does this cycle end? Part B: For the function y=cos x , the value      Log On


   

Question 1180524: Part A: For the function y=sin x , the value of 3pi over 2 is marked. At what point does this cycle end?
Part B: For the function y=cos x , the value of 2pi is marked. At what point did the cycle before this one begin?
Part C: Support your answers to Part A and Part B by showing all work.
Answer by ikleyn(52754) About Me  (Show Source):
You can put this solution on YOUR website!
Part A: For the function y=sin x , the value of 3pi over 2 is marked. At what point does this cycle end?
Part B: For the function y=cos x , the value of 2pi is marked. At what point did the cycle before this one begin?
Part C: Support your answers to Part A and Part B by showing all work.
~~~~~~~~~~~~~~~~


Let me re-write this post in CORRECT mathematical form. 


     Part A: For the function y=sin x , the value of 3pi over 2 is marked  and is considered as the beginning of the cycle. 
             At what point does this cycle end?

     Part B: For the function y=cos x , the value of 2pi is marked  and is considered as the end of the cycle. 
             At what point does the cycle start?

     
     Part C: Support your answers to Part A and Part B by showing all work.


Solution 

(A)  the function y = sin(x) has the period of  2pi.

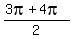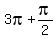     So, if the cycle starts at  3pi%2F2,  then it complets at  3pi%2F2+%2B+2pi = %283pi+%2B+4pi%29%2F2 = 7pi%2F2 = 3pi+%2B+pi%2F2.    ANSWER



(A)  the function y = cos(x) has the period of  2pi.

     So, if the cycle ends at  2pi,  then it starts at  2pi+-+2pi = 0.    ANSWER

Solved, answered and carefully explained.


/////////////


Writing in correct mathematical form MEANS that all necessary words are pronounced, so the meaning is totally clear;

and all unnecessary words absent - - - in order for do not create obstacles for freely flowing the thoughts.


Writing in correct mathematical style is the form of mathematical politeness and the way to express respect to the reader.