Question 1167604: Consider 
By finding the roots in cis form, and using appropriate substitutions, form, and using appropriate substitutions,
Show:
 =0 =0
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Consider  . .
By finding the roots in 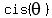 form, and using appropriate substitutions, show that form, and using appropriate substitutions, show that
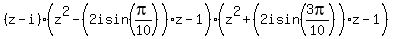 = 0. = 0.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Equation 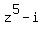 = 0 is the same as = 0 is the same as 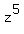 = i.
One root is, obviously, z = i, since = i.
One root is, obviously, z = i, since 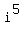 = i.
Let's list all the roots = i.
Let's list all the roots
 = = 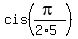 = =  , ,
 = = 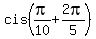 = = 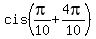 = = 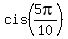 = = 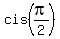 = i,
(we just noticed it above !) = i,
(we just noticed it above !)
 = =  = = 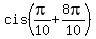 = =  , ,
 = =  = = 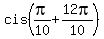 = = 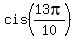 , ,
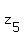 = = 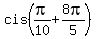 = = 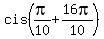 = =  .
Notice that .
Notice that  and and  have opposite real parts and identical imaginary parts. (*)
Similarly, have opposite real parts and identical imaginary parts. (*)
Similarly,  and and 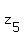 have opposite real parts and identical imaginary parts. (**)
We can write the decomposition of have opposite real parts and identical imaginary parts. (**)
We can write the decomposition of 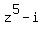 in the form of the product of linear binomials with the roots in the form of the product of linear binomials with the roots
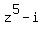 = = 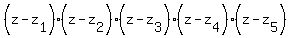 =
= =
= 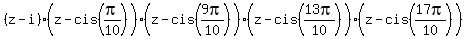 . (1)
In this decomposition (1), second and third parentheses will give the product . (1)
In this decomposition (1), second and third parentheses will give the product
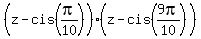 = = 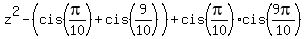 . (2)
Here . (2)
Here 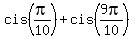 = = 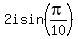 , as we noticed in (*), and , as we noticed in (*), and 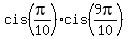 = = 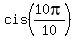 = = 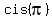 = -1.
Therefore, = -1.
Therefore,
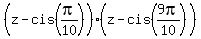 = =  .
Similarly, in decomposition (1), fourth and fifth parentheses will give the product .
Similarly, in decomposition (1), fourth and fifth parentheses will give the product
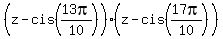 = = 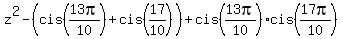 . (3)
Here . (3)
Here 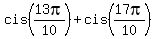 = =  , as we noticed in (**), and , as we noticed in (**), and 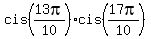 = = 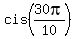 = = 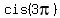 = -1.
Therefore, = -1.
Therefore,
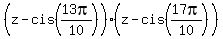 = = 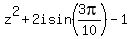 . (4)
Thus, combining everything in one piece, we get
If . (4)
Thus, combining everything in one piece, we get
If 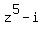 = 0, then = 0, then 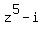 = =  = 0.
QED.
At this point, the proof is complete. = 0.
QED.
At this point, the proof is complete.
Solved.
////////////////////////////
In her post, @MathLover1 incorrectly read the problem and incorrectly understood
what the problem requested to prove.
So, her writing in her post is not a proof of the problem' statement
and has nothing in common with what this problem requests to prove.
For the peace in your mind, simply ignore that post.
|
|
|